
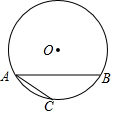
 如圖,已知⊙O的半徑長為25,弦AB長為48,C是弧AB的中點.求AC的長.
如圖,已知⊙O的半徑長為25,弦AB長為48,C是弧AB的中點.求AC的長. 分析 連接AO,由垂徑定理知OH⊥AB;在Rt△OAH中,易求OH長,進而易得HC的長.再利用勾股定理,即可得出AC的長.
解答 解:如圖,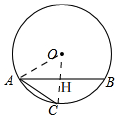 連接OA,OA交AB于H
連接OA,OA交AB于H
∵C是弧AB的中點,
∴OH⊥AB,
在Rt△OAH中,OA=25,AH=24,
根據勾股定理得:OH=$\sqrt{O{A}^{2}-A{H}^{2}}$=7,
∴HC=OC-OH=25-7=18,
在Rt△AHC中,根據勾股定理得:AC=$\sqrt{A{H}^{2}+H{C}^{2}}$=30,
∴AC的長為30.
點評 此題是垂徑定理,主要考查了勾股定理,以及垂徑定理,構造出Rt△OAH是解本題的關鍵.此類題目常用的方法是:弦的一半,弦心距,半徑構成的是直角三角形.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:選擇題
| A. | 19.6kg | B. | 20kg | C. | 19.7kg | D. | 20.2kg |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
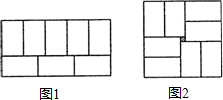 如圖所示,兩個圖案都是由8個大小一樣的小長方形拼成的,并且圖②中,中央小正方形的面積是1平方厘米.
如圖所示,兩個圖案都是由8個大小一樣的小長方形拼成的,并且圖②中,中央小正方形的面積是1平方厘米.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知在直角坐標系中,直角梯形OABC的直角腰在y軸上,底邊OC在x軸上,且∠BCO=45°,點B的坐標是(3,4).
如圖,已知在直角坐標系中,直角梯形OABC的直角腰在y軸上,底邊OC在x軸上,且∠BCO=45°,點B的坐標是(3,4).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com