
【題目】在平面直角坐標系中,二次函數y=x2+mx+2m﹣7的圖象經過點(1,0).
(1)求拋物線的表達式;
(2)把﹣4<x<1時的函數圖象記為H,求此時函數y的取值范圍;
(3)在(2)的條件下,將圖象H在x軸下方的部分沿x軸翻折,圖象H的其余部分保持不變,得到一個新圖象M.若直線y=x+b與圖象M有三個公共點,求b的取值范圍.

【答案】(1)拋物線的表達式為y=x2+2x﹣3;
(2)y的取值范圍是﹣4≤y<5;
(3)b的取值范圍是3<b<![]() .
.
【解析】試題分析:(1)把點(1,0)代入y=x2+mx+2m﹣7即可求得m的值,從而得二次函數的解析式;(2)求出當x=﹣1時和當x=﹣4時時y的值,根據函數的增減性確定y的取值范圍;(3)把拋物線y=x2+2x﹣3的圖象x軸下方的部分沿x軸翻折到x軸上方,則翻折部分的拋物線解析式為y=﹣(x+1)2+4(﹣3≤x≤1),當直線y=x+b經過(﹣3,0)時,直線y=x+b與圖象M有兩個公共點,此時b=3;當直線y=x+b與拋物線y=﹣(x+1)2+4(﹣3≤x≤1)相切時,直線y=x+b與圖象M有兩個公共點,即﹣(x+1)2+4=x+b有相等的實數解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=![]() .結合圖象可得,直線y=x+b與圖象M有三個公共點,b的取值范圍是3<b<
.結合圖象可得,直線y=x+b與圖象M有三個公共點,b的取值范圍是3<b<![]() .
.
試題解析:
(1)∵二次函數y=x2+mx+2m﹣7的圖象經過點(1,0),
∴1+m+2m﹣7=0,解得m=2,
∴拋物線的表達式為y=x2+2x﹣3;
(2)y=x2+2x﹣3=(x+1)2﹣4,
∵當﹣4<x<﹣1時,y隨x增大而減小;
當﹣1≤x<1時,y隨x增大而增大,
∴當x=﹣1,y最小=﹣4,
當x=﹣4時,y=5,
∴﹣4<x<1時,y的取值范圍是﹣4≤y<5;
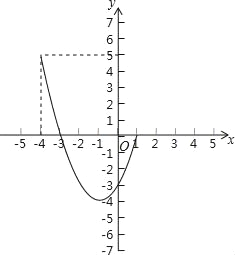
(3)y=x2+2x﹣3與x軸交于點(﹣3,0),(1,0),翻折后可得新圖象M如圖中紅色部分,
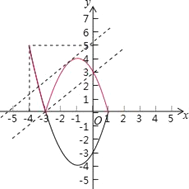
把拋物線y=x2+2x﹣3=(x+1)2﹣4的圖象x軸下方的部分沿x軸翻折到x軸上方,則翻折部分的拋物線解析式為y=﹣(x+1)2+4(﹣3≤x≤1),
當直線y=x+b經過(﹣3,0)時,直線y=x+b與圖象M有兩個公共點,此時b=3;
當直線y=x+b與拋物線y=﹣(x+1)2+4(﹣3≤x≤1)相切時,直線y=x+b與圖象M有兩個公共點,
即﹣(x+1)2+4=x+b有相等的實數解,整理得x2+3x+b﹣3=0,△=32﹣4(b﹣3)=0,解得b=![]() .
.
結合圖象可得,直線y=x+b與圖象M有三個公共點,b的取值范圍是3<b<![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+1經過點(2,6),且與直線y=![]() x+1相交于A,B兩點,點A在y軸上,過點B作BC⊥x軸,垂足為點C(4,0).
x+1相交于A,B兩點,點A在y軸上,過點B作BC⊥x軸,垂足為點C(4,0).

(1)求拋物線的解析式;
(2)若P是直線AB上方該拋物線上的一個動點,過點P作PD⊥x軸于點D,交AB于點E,求線段PE的最大值;
(3)在(2)的條件,設PC與AB相交于點Q,當線段PC與BE相互平分時,請求出點Q的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
材料1:對于一個關于![]() 的二次三項式
的二次三項式![]()
![]() ,除了可以利用配方法求請多項式的取值范圍外,愛思考的小川同學還想到了其他的方法:比如先令
,除了可以利用配方法求請多項式的取值范圍外,愛思考的小川同學還想到了其他的方法:比如先令![]()
![]() ,然后移項可得:
,然后移項可得:![]() ,再利用一元二次方程根的判別式來確定
,再利用一元二次方程根的判別式來確定![]() 的取值范圍,請仔細閱讀下面的例子:
的取值范圍,請仔細閱讀下面的例子:
例:求![]() 的取值范圍:
的取值范圍:
解:令![]()
∴![]()
∴![]()
∴![]()
∴![]() ;
;
材料2:在學習完一元二次方程的解法后,愛思考的小川同學又想到仿造一元二次方程的解法來解決一元二次不等式的解集問題,他的具體做法如下:
若關于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )有兩個不相等的實數根
)有兩個不相等的實數根![]() ,
,![]() (
(![]() )
)
則關于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集為:
)的解集為:![]() 或
或![]() .
.
則關于![]() 的一元二次不等式
的一元二次不等式![]() (
(![]() )的解集為:
)的解集為:![]() .
.
請根據上述材料,解答下列問題:
(1)若關于![]() 的二次三項式
的二次三項式![]() (
(![]() 為常數)的最小值為-6,則
為常數)的最小值為-6,則![]() ________;
________;
(2)求出代數式![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的代數式
的代數式![]() (其中
(其中![]() 、
、![]() 為常數,且
為常數,且![]() )的最小值為-4,最大值為7,請求出滿足條件的
)的最小值為-4,最大值為7,請求出滿足條件的![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=6,BC=4,過對角線BD中點O的直線分別交AB,CD邊于點E,F.
(1)求證:四邊形DEBF是平行四邊形;
(2)當四邊形DEBF是菱形時,求菱形的周長.
(3)在(2)的基礎上,直接寫出BD與EF的位置關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生手機使用情況,某學校開展了“手機伴我健康行”主題活動,他們隨機抽取部分學生進行“使用手機目的”和“每周使用手機的時間”的問卷調查,并繪制成如圖①,②的統計圖,已知“查資料”的人數是40人.
使用手機的目的 每周使用手機的時間

(0~1表示大于0同時小于等于1,以此類推)
請你根據以上信息解答下列問題:
(1)在扇形統計圖中,“玩游戲”對應的百分比為_______,圓心角度數是度_______;
(2)補全條形統計圖:
(3)該校共有學生2100人,估計每周使用手機時間在2小時以上(不含2小時)的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】【發現證明】
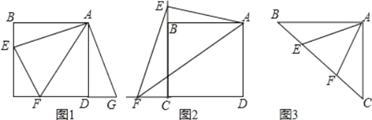
如圖1,點E,F分別在正方形ABCD的邊BC,CD上,∠EAF=45°,試判斷BE,EF,FD之間的數量關系.
小聰把△ABE繞點A逆時針旋轉90°至△ADG,通過證明△AEF≌△AGF;從而發現并證明了EF=BE+FD.
【類比引申】
(1)如圖2,點E、F分別在正方形ABCD的邊CB、CD的延長線上,∠EAF=45°,連接EF,請根據小聰的發現給你的啟示寫出EF、BE、DF之間的數量關系,并證明;
【聯想拓展】
(2)如圖3,如圖,∠BAC=90°,AB=AC,點E、F在邊BC上,且∠EAF=45°,若BE=3,EF=5,求CF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,在一個盒子里有紅球和白球共10個,它們除顏色外都相同,將它們充分搖勻后,從中隨機抽出一個,記下顏色后放回.在摸球活動中得到如下數據:
摸球總次數 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
摸到紅球的頻數 | 17 | 32 | 44 | 64 | 78 |
| 103 | 122 | 136 | 148 |
摸到紅球的頻率 | 0.34 | 0.32 | 0.293 | 0.32 | 0.312 | 0.32 | 0.294 |
| 0.302 |
|
(1)請將表格中的數據補齊;
(2)根據上表,完成折線統計圖;
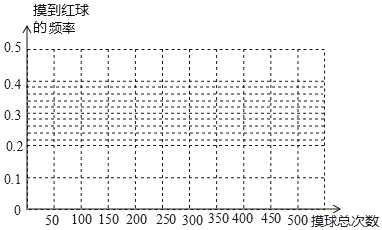
(3)請你估計,當摸球次數很大時,摸到紅球的頻率將會接近 (精確到0.1).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】感恩節即將來臨,小王調查了初三年級部分同學在感恩節當天將以何種方式對幫助過自己的人表達感謝,他將調查結果分為如下四類:A類﹣﹣當面表示感謝、B類﹣﹣打電話表示感謝、C類﹣﹣發短信表示感謝、D類﹣﹣寫書信表示感謝.他將調查結果繪制成了如圖所示的扇形統計圖和條形統計圖.請你根據圖中提供的信息完成下列各題:
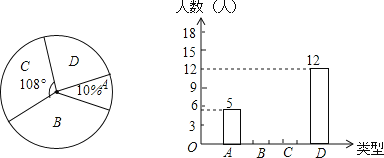
(1)補全條形統計圖;
(2)在A類的同學中,有4人來自同一班級,其中有2人主持過班會.現準備從他們4人中隨機抽出兩位同學主持感恩節主題班會課,請用樹狀圖或列表法求抽出1人主持過班會而另一人沒主持過班會的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com