
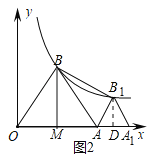
【題目】如圖1,反比例函數![]() (k>0)圖象經過等邊△OAB的一個頂點B,點A坐標為(2,0),過點B作BM⊥x軸,垂足為M.
(k>0)圖象經過等邊△OAB的一個頂點B,點A坐標為(2,0),過點B作BM⊥x軸,垂足為M.
(1)求點B的坐標和k的值;
(2)若將△ABM沿直線AB翻折,得到△ABM',判斷該反比例函數圖象是從點M'的上方經過,還是從點M'的下方經過,又或是恰好經過點M',并說明理由;
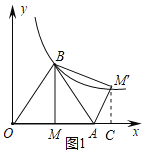
(3)如圖2,在x軸上取一點A1,以AA1為邊長作等邊△AA1B1,恰好使點B1落在該反比例函數圖象上,連接BB1,求△ABB1的面積.

【答案】(1)k=![]() ;(2)該反比例函數圖象是從點M'的下方經過;理由見解析;(3)△ABB1的面積為
;(2)該反比例函數圖象是從點M'的下方經過;理由見解析;(3)△ABB1的面積為![]() .
.
【解析】
(1)由△OAB為等邊三角形及OA=2,可得出OM,BM的長,進而可得出點B的坐標,由點B的坐標利用反比例函數圖象上點的坐標特征可求出k的值;
(2)過點M′作M′C⊥x軸,垂足為點C,由折疊的性質,可知:AM′=AM=1,∠BAM′=∠BAM=60°,在Rt△ACM′中,通過解直角三角形可求出AC,CM′的長,進而可得出OC的長,利用反比例函數圖象上點的坐標特征可求出反比例函數圖象與直線CM′交點的縱坐標,將其與點M′的縱坐標比較后即可得出結論;
(3)過點B1作B1D⊥x軸,垂足為點D,設AA1=a,則AD=![]() a,B1D=
a,B1D=![]() a,OD=2+
a,OD=2+![]() a,進而可得出點B1的坐標,利用反比例函數圖象上點的坐標特征可求出a的值,進而可得出MD,B1D,AD的長,再結合S△ABB1=S梯形BMDB1S△BMAS△ADB1即可求出△ABB1的面積.
a,進而可得出點B1的坐標,利用反比例函數圖象上點的坐標特征可求出a的值,進而可得出MD,B1D,AD的長,再結合S△ABB1=S梯形BMDB1S△BMAS△ADB1即可求出△ABB1的面積.
(1)∵△OAB為等邊三角形,OA=2,
∴OM=![]() OA=1,BM=
OA=1,BM=![]() OA=
OA=![]() ,
,
∴點B的坐標為(1,![]() ).
).
∵反比例函數![]() 圖象經過點B,
圖象經過點B,
∴k=![]() .
.
(2)該反比例函數圖象是從點M'的下方經過,理由如下:
過點M′作M′C⊥x軸,垂足為點C,如圖1所示.
由折疊的性質,可知:AM′=AM=1,∠BAM′=∠BAM=60°,
∴∠M′AC=180°﹣∠BAM﹣∠BAM′=60°.
在Rt△ACM′中,AM′=1,∠ACM′=90°,∠M′AC=60°,
∴∠AM′C=30°,
∴AC=![]() AM′=
AM′=![]() ,CM′=
,CM′=![]() AM′=
AM′=![]() .
.
∴OC=OA+AC=![]() ,
,
∴點M′的坐標為(![]() ,
,![]() ).
).
當x=![]() 時,
時,![]() ,
,
∵![]() <
<![]() ,
,
∴該反比例函數圖象是從點M'的下方經過.
(3)過點B1作B1D⊥x軸,垂足為點D,如圖2所示.
設AA1=a,則AD=![]() a,B1D=
a,B1D=![]() a,OD=2+
a,OD=2+![]() a,
a,
∴點B1的坐標為(2+![]() a,
a,![]() a).
a).
∵點B1在該反比例函數![]() 的圖象上,
的圖象上,
∴(2+![]() a)
a)![]() a=
a=![]() ,
,
解得:a1=﹣2![]() ﹣2(舍去),a2=2
﹣2(舍去),a2=2![]() ﹣2,
﹣2,
∴MD=AM+AD=![]() ,B1D=
,B1D=![]() a=
a=![]() ﹣
﹣![]() ,AD=
,AD=![]() a=
a=![]() ﹣1,
﹣1,
∴S△ABB1=S梯形BMDB1S△BMAS△ADB1
=![]() (BM+B1D)MD﹣
(BM+B1D)MD﹣![]() BMAM﹣
BMAM﹣![]() B1DAD,
B1DAD,
![]() ,
,
![]() .
.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線y=x2-2x-1交y軸于點A,過點A作AB∥x軸交拋物線于點B,點P在拋物線上,連結PA、PB,若點P關于x軸的對稱點恰好落在直線AB上,則△ABP的面積是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
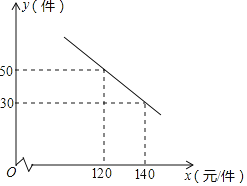
【題目】某商場購進一種每件價格為90元的新商品,在商場試銷時發現:銷售單價![]() 元
元![]() 件
件![]() 與每天銷售量
與每天銷售量![]() 件
件![]() 之間滿足如圖所示的關系.
之間滿足如圖所示的關系.
![]() 求出y與x之間的函數關系式;
求出y與x之間的函數關系式;
![]() 寫出每天的利潤W與銷售單價x之間的函數關系式,并求出售價定為多少時,每天獲得的利潤最大?最大利潤是多少?
寫出每天的利潤W與銷售單價x之間的函數關系式,并求出售價定為多少時,每天獲得的利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() 和一次函數y=kx﹣1的圖象都經過點P(m,﹣3m).
和一次函數y=kx﹣1的圖象都經過點P(m,﹣3m).
(1)求點P的坐標和這個一次函數的解析式;
(2)若點M(a,y1)和點N(a+1,y2)都在這個一次函數的圖象上.試通過計算或利用一次函數的性質,說明y1大于y2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課上,甲、乙、丙、丁四位同學共同研究二次函數y=x2﹣2x+c(c是常數).甲發現:該函數的圖象與x軸的一個交點是(﹣2,0);乙發現:該函數的圖象與y軸的交點在(0,﹣4)上方;丙發現:無論x取任何值所得到的y值總能滿足c﹣y≤1;丁發現:當﹣1<x<0時,該函數的圖象在x軸的下方,當3<x<4時,該函數的圖象在x軸的上方.通過老師的最后評判得知這四位同學中只有一位同學發現的結論是錯誤的,則該同學是( )
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DCB中,AB = DC,AC = DB,AC與DB交于點M.

【1】求證:△ABC≌△DCB
【2】過點C作CN∥BD,過點B作BN∥AC,CN與BN交于點N,試判斷線段BN與CN的數量關系,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
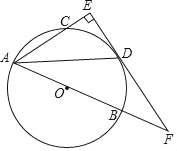
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,∠CAB的平分線交⊙O于點D,過點D作ED⊥AE,垂足為E,交AB的延長線于F.
(1)求證:ED是⊙O的切線;
(2)若AD=4![]() ,AB=6,求FD的長.
,AB=6,求FD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知□ABCD的兩邊AB、BC的長是關于x的一元二次方程方程![]() 的兩個實數根.
的兩個實數根.
(1)試說明:無論m取何值,原方程總有兩個實數根;
(2)當m為何值時,□ABCD是菱形?求出這時菱形的邊長;
(3)若AB﹦2,求BC的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com