【題目】計算：（ 
）﹣1+（3﹣π）°﹣|1﹣tan60°|+ 
÷2．
【答案】解：原式=2+1﹣ 
+1+ =4
【解析】原式利用零指數冪、負整數指數冪法則，絕對值的代數意義，以及二次根式性質計算即可得到結果．
【考點精析】關于本題考查的整數指數冪的運算性質和特殊角的三角函數值，需要了解aman=am+n(m、n是正整數)；（am）n=amn(m、n是正整數)；(ab)n=anbn(n是正整數)；am/an=am-n(a不等于0，m、n為正整數）；（a/b）n=an/bn(n為正整數)；分母口訣：30度、45度、60度的正弦值、余弦值的分母都是2，30度、45度、60度的正切值、余切值的分母都是3，分子口訣：“123，321，三九二十七”才能得出正確答案．
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，A、B兩點分別在x軸和y軸上，OA=1，OB= 
，連接AB，過AB中點C1分別作x軸和y軸的垂線，垂足分別是點A1、B1 ， 連接A1B1 ， 再過A1B1中點C2作x軸和y軸的垂線，照此規律依次作下去，則點Cn的坐標為 ．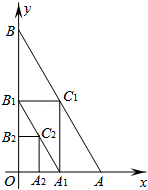 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知點P（x0 ， y0）和直線y=kx+b，則點P到直線y=kx+b的距離d可用公式d= 
計算． 例如：求點P（﹣1，2）到直線y=3x+7的距離．
解：因為直線y=3x+7，其中k=3，b=7．
所以點P（﹣1，2）到直線y=3x+7的距離為d= 
= 
= 
．
根據以上材料，解答下列問題：
（1）點P（1，﹣1）到直線y=x+1的距離；
（2）已知⊙Q的圓心Q的坐標為（0，4），半徑r為2，判斷⊙Q與直線y= 
x+8的位置關系并說明理由；
（3）已知直線y=﹣2x+1與y=﹣2x+6平行，A、B是直線y=﹣2x+1上的兩點且AB=8，P是直線y=﹣2x+6上任意一點，求△PAB的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
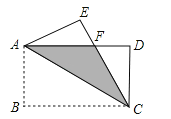
【題目】如圖，將矩形ABCD沿對角線AC翻折，點B落在點F處，FC交AD于E．
（1）求證：△AFE≌△CDF；
（2）若AB=4，BC=8，求圖中陰影部分的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】(1)填表：
a | 0.000 001 | 0.001 | 1 | 1 000 | 1 000 000 |
|
(2)由上表你發現了什么規律?請用語言敘述這個規律：______________________________.
(3)根據你發現的規律填空：
①已知
=1.442,則
=__________,
=__________；
②已知
=0.076 96,則
=__________.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司在工程招標時，接到甲、乙兩個工程隊的投標書．每施工一天，需付甲工程隊工程款1.5萬元，付乙工程隊工程款1.1萬元，工程領導小組根據甲、乙兩隊的投標書測算，形成下列三種施工方案：
方案①：甲隊單獨完成此項工程剛好如期完工；
方案②：乙隊單獨完成此項工程要比規定工期多用5天；
方案③：若甲、乙兩隊合作4天，剩下的工程由乙隊獨做也正好如期完工；
（1）求甲、乙兩隊單獨完成此項工程各需多少天？
（2）如果工程不能如期完工，公司每天將損失3000元，如果你是公司經理，你覺得哪一種施工方案劃算，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一個盒子里有完全相同的三個小球，球上分別標上數字﹣1、1、2．隨機摸出一個小球（不放回）其數字記為p，再隨機摸出另一個小球其數字記為q，則滿足關于x的方程x2+px+q=0有實數根的概率是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解某市初三學生的體育測試成績和課外體育鍛煉時間的情況，現從全市初三學生體育測試成績中隨機抽取120名學生的體育測試成績作為樣本.體育成績分為四個等次：優秀、良好、及格、不及格.
（1）試求樣本扇形圖中體育成績“良好”所對扇形圓心角的度數；
（2）統計樣本中體育成績“優秀”和“良好”學生課外體育鍛煉時間表（如圖表所示），請將圖表填寫完整（記學生課外體育鍛煉時間為
小時）；
（3）全市初三學生中有14400人的體育測試成績為“優秀”和“良好”，請估計這些學生中課外體育鍛煉時間不少于4小時的學生人數.
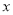
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
