
| 1 |
| 2 |

| ||
| 2 |
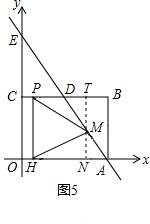
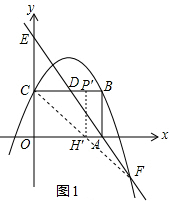 解:(1)∵矩形ABCO,B點坐標為(4,3),拋物線y=-
解:(1)∵矩形ABCO,B點坐標為(4,3),拋物線y=-| 1 |
| 2 |
| 1 |
| 2 |
|
|
| 1 |
| 2 |
|
|
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
|
|
| AM |
| AE |
| AN |
| AO |
| MN |
| EO |
| 13 |
| ||||
2
|
| AN |
| 4 |
| MN |
| 6 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 14 |
| 25 |
| 3 |
| 2 |
| 3 |
| 2 |
| 16 |
| 5 |
| 4 |
| 5 |
| 14 |
| 25 |
| 4 |
| 5 |
| 16 |
| 5 |


科目:初中數學 來源: 題型:
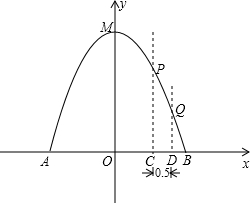 的體積和圓柱形桶的厚度忽略不計),以M點為頂點,拋物線對稱軸為y軸,水平地面為x軸建立平面直角坐標系.
的體積和圓柱形桶的厚度忽略不計),以M點為頂點,拋物線對稱軸為y軸,水平地面為x軸建立平面直角坐標系.查看答案和解析>>
科目:初中數學 來源: 題型:
 水柱在與池中心的水平距離為1m處達到最高,高度為3m.
水柱在與池中心的水平距離為1m處達到最高,高度為3m.查看答案和解析>>
科目:初中數學 來源: 題型:

| 多面體 | 面數a | 展開圖的頂點數b | 展開圖的棱數c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱錐 | 5 5 |
8 | 12 |
| 立方體 | 6 6 |
14 14 |
19 19 |
查看答案和解析>>
科目:初中數學 來源:學習周報 數學 華師大八年級版 2009-2010學年 第13期 總第169期 華師大版 題型:044
工具閱讀:
在平面上畫兩條原點重合、互相垂直且具有相同單位長度的數軸(如圖),這就建立了平面直角坐標系.通常把其中水平的一條數軸叫做x軸或橫軸,取向右為正方向;鉛直的數軸叫做y軸或縱軸,取向上為正方向;兩數軸的交點O叫做坐標原點.

問題探究:如圖1,在6×6的方格紙中,給出如下三種變換:P變換,Q變換,R變換.

將圖形F沿x軸向右平移1格得圖形F1,稱為作1次P變換;
將圖形F沿y軸翻折得圖形F2,稱為作1次Q變換;
將圖形F繞坐標原點順時針旋轉90°得圖形F3,稱為作1次R變換.
規定:PQ變換表示先作1次Q變換,再作1次P變換;QP變換表示先作1次P變換,再作1次Q變換;Rn變換表示作n次R變換.
解答下列問題:
(1)作R4變換相當于至少作________次Q變換;
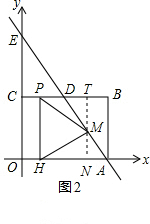
(2)請在圖2中畫出圖形F作R2011變換后得到的圖形F4;

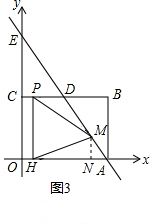
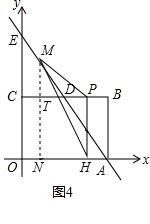
(3)PQ變換與QP變換是否是相同的變換?請在圖3中畫出PQ變換后得到的圖形F5,在圖4中畫出QP變換后得到的圖形F6.

查看答案和解析>>
科目:初中數學 來源:2011-2012學年重慶市南開中學九年級(上)第一次月考數學試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com