
【題目】在△ABC中,CA=CB,∠ACB=α(0°<α<180°).點P是平面內不與A,C重合的任意一點,連接AP,將線段AP繞點P逆時針旋轉α得到線段DP,連接AD,CP.點M是AB的中點,點N是AD的中點.
(1)問題發現:如圖1,當α=60°時,![]() 的值是 ,直線MN與直線PC相交所成的較小角的度數是 .
的值是 ,直線MN與直線PC相交所成的較小角的度數是 .
(2)類比探究:如圖2,當α=120°時,請寫出的![]() 值及直線MN與直線PC相交所成的較小角的度數,并就圖2的情形說明理由.
值及直線MN與直線PC相交所成的較小角的度數,并就圖2的情形說明理由.
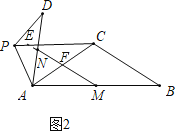
(3)解決問題:如圖3,當α=90°時,若點E是CB的中點,點P在直線ME上,請直接寫出點B,P,D在同一條直線上時![]() 的值.
的值.
【答案】(1)![]() ,60°;(2)
,60°;(2)![]() ,30°,見解析;(3)當點P在線段BD上時,
,30°,見解析;(3)當點P在線段BD上時, ![]() ,當點P在DB延長線上時,
,當點P在DB延長線上時,![]() =2+
=2+![]() .
.
【解析】
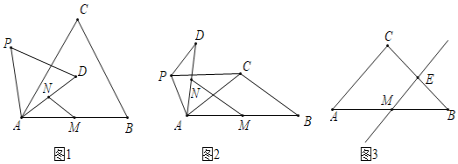
(1)如圖1中,連接PC,BD,延長BD交PC于K,交AC于G.證明△PAC≌△DAB(SAS),利用全等三角形的性質以及三角形的中位線定理即可解決問題.
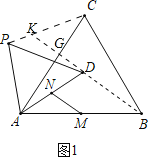
(2)如圖設MN交AC于F,延長MN交PC于E.證明△ACP∽△AMN,推出∠ACP=∠AMN,![]() 可得結論.
可得結論.
(3)分兩種情形分別畫出圖形,利用三角形中位線定理即可解決問題.
解:(1)如圖1中,連接PC,BD,延長BD交PC于K,交AC于G.
∵CA=CB,∠ACB=60°,
∴△ABC是等邊三角形,
∴∠CAB=∠PAD=60°,AC=AB,
∴∠PAC=∠DAB,
∵AP=AD,
∴△PAC≌△DAB(SAS),
∴PC=BD,∠ACP=∠ABD,
∵AN=ND,AM=BM,
∴BD=2MN,
∴![]() .
.
∵∠CGK=∠BGA,∠GCK=∠GBA,
∴∠CKG=∠BAG=60°,
∴BK與PC的較小的夾角為60°,
∵MN∥BK,
∴MN與PC較小的夾角為60°.
故答案為![]() ,60°.
,60°.
(2)如圖設MN交AC于F,延長MN交PC于E.
∵CA=CB,PA=PD,∠APD=∠ACB=120°,
∴△PAD∽△CAB,
∴![]() ,
,
∵AM=MB,AN=ND,
∴![]() ,
,
∴△ACP∽△AMN,
∴∠ACP=∠AMN, ![]() ,
,
∵∠CFE=∠AFM,
∴∠FEC=∠FAM=30°.
(3)設MN=a,由(2)得![]() ,
,
∵∠ACB=90°,△ABC為等腰直角三角形,
∴AC=![]() AM
AM
∴![]() ,
,
∴PC=![]() a,
a,
∵ME是△ABC的中位線,∠ACB=90°,
∴ME是線段BC的中垂線,
∴PB=PC=![]() a,
a,
∵MN是△ADB的中位線,
∴DB=2MN=2a,
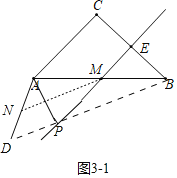
如圖3﹣1中,當點P在線段BD上時,PD=DB﹣PB=(2﹣![]() )a,
)a,
∴![]() .
.
如圖3﹣2中,當點P在DB延長線上時,PD=DB+PB=(2+![]() )a,
)a,
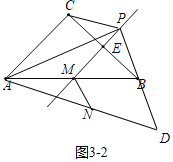
∴![]() =2+
=2+![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某商店購進一批成本為每件30元的商品,商店按單價不低于成本價,且不高于50元銷售.經調查發現,該商品每天的銷售量y(件)與銷售單價x(元)之間滿足一次函數關系,其圖象如圖所示.
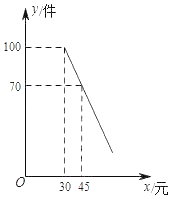
(1)求該商品每天的銷售量y(件)與銷售單價x(元)之間的函數關系式;
(2)銷售單價定為多少元時,才能使銷售該商品每天獲得的利潤w(元)最大?最大利潤是多少?
(3)若商店要使銷售該商品每天獲得的利潤高于800元,請直接寫出每天的銷售量y(件)的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發商銷售每箱進價為40元的柑橘,物價部門規定每箱售價不得高于55元;市場調查發現,若每箱以45元的價格銷售,平均每天銷售105箱;每箱以50元的價格銷售,平均每天銷售90箱.假定每天銷售量y(箱)與銷售價x(元/箱)之間滿足一次函數關系式.
(1)求平均每天銷售量y(箱)與銷售價x(元/箱)之間的函數關系式;
(2)求該批發商平均每天的銷售利潤w(元)與銷售價x(元/箱)之間的函數關系式;
(3)當每箱蘋果的銷售價為多少元時,可以獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明想測量一棵樹的高度,他發現樹的影子恰好落在地面和一斜坡上;如圖,此時測得地面上的影長為8米,坡面上的影長為4米.已知斜坡的坡角為300,同一時 刻,一根長為l米、垂直于地面放置的標桿在地面上的影長為2米,則樹的高度為【 】
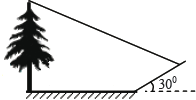
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,已知AB=2,點E是BC邊的中點,連接AE,△AB′E和△ABE關于AE所在直線對稱,若△B′CD是直角三角形,則BC邊的長為_____.
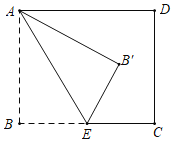
查看答案和解析>>
科目:初中數學 來源: 題型:
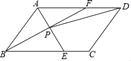
【題目】如圖,平行四邊形ABCD中,AB=4,AD=6,∠ABC=60°,∠BAD與∠ABC的平分線AE、BF交于點P,連接PD,則tan∠ADP的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:點A與⊙O上所有點的連線段中,長度的最小值稱為點A到⊙O的最小距離,記為mA;點A與⊙O上所有點的連線段中,長度的最大值稱為點A到⊙O的最大距離,記為MA,如圖,⊙O的半徑為r,點A在⊙O外,且OA=d,則mA=d﹣r.證明如下:
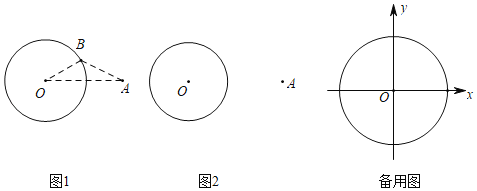
證明:如圖1,設B為圓上任意一點,連結OA、OB、AB
①當O、A、B不共線時,AB>OA﹣OB
即AB>d﹣r
②當O、A、B共線時,AB=OA﹣OB
即AB=d﹣r
綜上,AB≥d﹣r,即mA=d﹣r
(1)利用剛才的證明,結合所給的圖2,⊙O的半徑為r,點A在⊙O外,且OA=d,探究MA,你的結論是MA= ,請證明你的結論;
(2)已知⊙O的半徑為2,mA=4,則MA= ;
(3)在平面直角坐標系中,以原點O為圓心,6為半徑作⊙O,第二象限的點A的坐標為(﹣3,a),且mA=1,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,C分別在x軸,y軸上,四邊形ABCO為矩形,AB=16,點D與點A關于y軸對稱,tan∠ACB=![]() ,點E、F分別是線段AD、AC上的動點,(點E不與點A,D重合),且∠CEF=∠ACB.
,點E、F分別是線段AD、AC上的動點,(點E不與點A,D重合),且∠CEF=∠ACB.
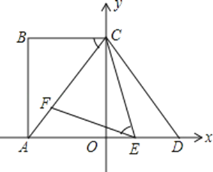
(1)求AC的長和點D的坐標;
(2)求證:![]() ;
;
(3)當△EFC為等腰三角形時,求點E的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com