
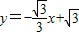 分別與x軸、y軸交于A、B兩點(diǎn),⊙E經(jīng)過(guò)原點(diǎn)O及A、B兩點(diǎn),C是⊙E上一點(diǎn),連接BC交OA于點(diǎn)D,∠COD=∠CBO.
分別與x軸、y軸交于A、B兩點(diǎn),⊙E經(jīng)過(guò)原點(diǎn)O及A、B兩點(diǎn),C是⊙E上一點(diǎn),連接BC交OA于點(diǎn)D,∠COD=∠CBO.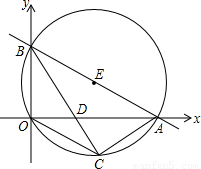
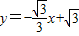 分別與x軸、y軸交于A、B兩點(diǎn),即可求得點(diǎn)A與點(diǎn)B的坐標(biāo),然后連接EC,交x軸于點(diǎn)H,由∠COD=∠CBO,根據(jù)垂徑定理的即可求得OH與AH的長(zhǎng),由勾股定理,可求得AB的長(zhǎng),EH的長(zhǎng),繼而求得點(diǎn)C的坐標(biāo);
分別與x軸、y軸交于A、B兩點(diǎn),即可求得點(diǎn)A與點(diǎn)B的坐標(biāo),然后連接EC,交x軸于點(diǎn)H,由∠COD=∠CBO,根據(jù)垂徑定理的即可求得OH與AH的長(zhǎng),由勾股定理,可求得AB的長(zhǎng),EH的長(zhǎng),繼而求得點(diǎn)C的坐標(biāo);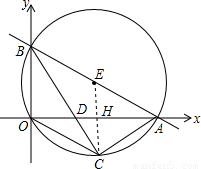 (1)解:∵直線(xiàn)
(1)解:∵直線(xiàn)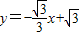 分別與x軸、y軸交于A、B兩點(diǎn),
分別與x軸、y軸交于A、B兩點(diǎn),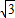 ,當(dāng)y=0時(shí),x=3,
,當(dāng)y=0時(shí),x=3,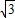 ),
),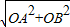 =2
=2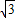 ,
, AB=
AB=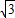 ,
,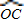 =
=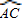 ,
, OA=
OA= ,
, =
=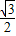 ,
,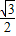 ,
, ,-
,-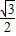 );
); ,-
,-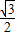 );
);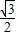 =a×
=a× ×(
×( -3),
-3),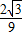 ,
,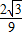 x2-
x2-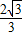 x;
x; =
=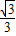 ,
,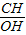 =
= ,
,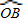 =
=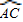 ,
,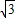 ,
, ≠AB,
≠AB,
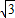 ,
, ,
,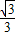 ×
× +
+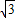 =
=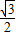 ,
, ,
,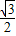 ).
).

 陽(yáng)光考場(chǎng)單元測(cè)試卷系列答案
陽(yáng)光考場(chǎng)單元測(cè)試卷系列答案 名校聯(lián)盟沖刺卷系列答案
名校聯(lián)盟沖刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 已知:如圖,直線(xiàn)y=-x+4分別與x軸,y軸交于A、B兩點(diǎn),從點(diǎn)P(2,0)射出的光線(xiàn)經(jīng)直線(xiàn)AB反射后再射到直線(xiàn)OB上,最后經(jīng)直線(xiàn)OB反射后又回到P點(diǎn),則光線(xiàn)所經(jīng)過(guò)的路程是( )
已知:如圖,直線(xiàn)y=-x+4分別與x軸,y軸交于A、B兩點(diǎn),從點(diǎn)P(2,0)射出的光線(xiàn)經(jīng)直線(xiàn)AB反射后再射到直線(xiàn)OB上,最后經(jīng)直線(xiàn)OB反射后又回到P點(diǎn),則光線(xiàn)所經(jīng)過(guò)的路程是( )A、2
| ||
| B、6 | ||
C、3
| ||
D、4+2
|
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 B,⊙P經(jīng)過(guò)點(diǎn)A、點(diǎn)B(圓心P在x軸負(fù)半軸上),已知AB=10,AP=
B,⊙P經(jīng)過(guò)點(diǎn)A、點(diǎn)B(圓心P在x軸負(fù)半軸上),已知AB=10,AP=| 25 | 4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
 (2012•青浦區(qū)二模)如圖,直線(xiàn)y=x+1分別與 x軸、y軸分別相交于點(diǎn)A、B.拋物線(xiàn)y=ax2+bx+c(a≠0)與 y軸的正半軸相交于點(diǎn)C,與這個(gè)一次函數(shù)的圖象相交于A、D,且sin∠ACB=
(2012•青浦區(qū)二模)如圖,直線(xiàn)y=x+1分別與 x軸、y軸分別相交于點(diǎn)A、B.拋物線(xiàn)y=ax2+bx+c(a≠0)與 y軸的正半軸相交于點(diǎn)C,與這個(gè)一次函數(shù)的圖象相交于A、D,且sin∠ACB=
| ||
| 10 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
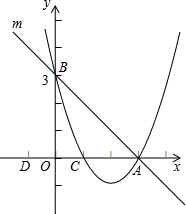 (2013•澄江縣二模)如圖,已知:直線(xiàn)m分別與x軸、y軸相交于A、B兩點(diǎn),拋物線(xiàn)y=ax2+bx+c經(jīng)過(guò)A(3,0)、B(0,3)、C(1,0)三點(diǎn).
(2013•澄江縣二模)如圖,已知:直線(xiàn)m分別與x軸、y軸相交于A、B兩點(diǎn),拋物線(xiàn)y=ax2+bx+c經(jīng)過(guò)A(3,0)、B(0,3)、C(1,0)三點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:044
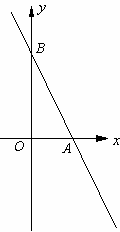
如圖,直線(xiàn)![]() 分別與x軸、y軸相交于A、B兩點(diǎn),O為坐標(biāo)原點(diǎn),A點(diǎn)的坐標(biāo)為(4,0)。
分別與x軸、y軸相交于A、B兩點(diǎn),O為坐標(biāo)原點(diǎn),A點(diǎn)的坐標(biāo)為(4,0)。
⑴求k的值;
⑵若P為y軸(B點(diǎn)除外)上的一點(diǎn),過(guò)P作PC⊥y軸交直線(xiàn)AB于C,設(shè)線(xiàn)段PC的長(zhǎng)為l,點(diǎn)P的坐標(biāo)為(0,m)。
①如果點(diǎn)P在線(xiàn)段OB(B點(diǎn)除外)上移動(dòng),求l與m的函數(shù)關(guān)系式,并寫(xiě)出自變量m的取值范圍;
②如果點(diǎn)P在射線(xiàn)BO(B、O兩點(diǎn)除外)上移動(dòng),連結(jié)PA,則△APC的面積S也隨之發(fā)生變化。請(qǐng)你在面積S的整個(gè)變化過(guò)程中,求當(dāng)m為何值時(shí),S=4。
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com