
【題目】記多項式x2+2x+1為 f(x),多項式y2-4y+4為f(y),且多項式f(x)的項數為a,f(y)的次數、一次項系數分別是b、m,數a,b,m數軸上分別對應著點A,B,M.
(1)求代數式a2-b2的值;
(2)數軸上有一點G,且到點M,B的距離相等.
①求線段GA的長;
②若n是關于x的方程mx+b=ax的解,且數軸上點N對應著數n,比較線段NG與NB的大小.
【答案】(1)5;(2)①線段GA的長為4;②NB>NG.
【解析】
(1)根據多項式的項數、次數的定義得到a,b的值,然后代入求值;
(2)首先求出點G表示的數,然后再求線段GA的長;
(3)將a=3,b=2,m=-4代入方程并求解,即可得到數軸上點N對應的數n,然后分別計算出線段NG和線段NB的長,比較即可.
解:(1)由題意可得:a=3,b=2,m=-4,
∴a2-b2=9-4=5;
(2)①∵點G到點M,B的距離相等,
∴點G表示的數為:![]() ,
,
∴線段GA的長為:3-(-1)=4;
②由題意可知,該方程為:-4x+2=3x,
解得:![]() ,即數軸上點N對應的數n
,即數軸上點N對應的數n![]() ,
,
∴線段NG的長為:![]() ,
,
線段NB的長為:![]() ,
,
∴NB>NG.


科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣![]() (x+1)(x﹣3)與x軸交于A、B兩點,與y軸交于點C,點D為該拋物線的對稱軸上一點,當點D到直線BC和到x軸的距離相等時,則點D的坐標為 .
(x+1)(x﹣3)與x軸交于A、B兩點,與y軸交于點C,點D為該拋物線的對稱軸上一點,當點D到直線BC和到x軸的距離相等時,則點D的坐標為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a,b,c為常數,且a≠0)中的x與y的部分對應值如下表:
X | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列結論:
⑴ac<0;
⑵當x>1時,y的值隨x值的增大而減小.
⑶3是方程ax2+(b﹣1)x+c=0的一個根;
⑷當﹣1<x<3時,ax2+(b﹣1)x+c>0.
其中正確的個數為()
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣x2+bx+c上部分點的橫坐標x,縱坐標y的對應值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
從上表可知,下列說法中,錯誤的是( )
A. 拋物線與x軸的一個交點坐標為(﹣2,0) B. 拋物線與y軸的交點坐標為(0,6)
C. 拋物線的對稱軸是直線x=0 D. 拋物線在對稱軸左側部分是上升的
查看答案和解析>>
科目:初中數學 來源: 題型:
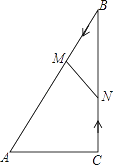
【題目】如圖,在![]() 中,
中,![]() ,動點
,動點![]() 從點
從點![]() 出發, 在
出發, 在![]() 邊上以每秒
邊上以每秒![]() 的速度向點
的速度向點![]() 勻速運動,同時動點
勻速運動,同時動點![]() 從點
從點![]() 出發,在
出發,在![]() 邊上以每秒
邊上以每秒![]() 的速度向點
的速度向點![]() 勻速運動,設運動時間為
勻速運動,設運動時間為![]() 秒
秒![]() ,連接
,連接![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 與
與![]() 相似,求
相似,求![]() 的值;
的值;
![]() 當
當![]() 為何值時,四邊形
為何值時,四邊形![]() 的面積為
的面積為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:求1+2+22+23+24+…+22019的值.
解:設S=1+2+22+23+24+…+22019,將等式兩邊同時乘以2得:2S=2+22+23+24+25+…+22019+22020
將下式減去上式得2S-S=22020-1
即S=22020-1
即1+2+22+23+24+…=22020-1
請你仿照此法計算:
(1)1+2+22+23+24+…+220
(2)1+5+52+53+54+…+5n(其中n為正整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自主學習,請閱讀下列解題過程.
解一元二次不等式:x2﹣5x>0.
解:設x2﹣5x=0,解得:x1=0,x2=5,則拋物線y=x2﹣5x與x軸的交點坐標為(0,0)和(5,0).畫出二次函數y=x2﹣5x的大致圖象(如圖所示),由圖象可知:當x<0,或x>5時函數圖象位于x軸上方,此時y>0,即x2﹣5x>0,所以,一元二次不等式x2﹣5x>0的解集為:x<0,或x>5.
通過對上述解題過程的學習,按其解題的思路和方法解答下列問題:
(1)上述解題過程中,滲透了下列數學思想中的 和 .(只填序號)
①轉化思想 ②分類討論思想 ③數形結合思想
(2)一元二次不等式x2﹣5x<0的解集為 .
(3)用類似的方法解一元二次不等式:x2﹣2x﹣3>0.
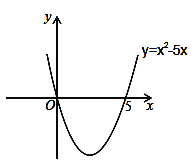
查看答案和解析>>
科目:初中數學 來源: 題型:
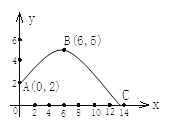
【題目】在體育測試時,初三的一名高個子男生推鉛球,已知鉛球所經過的路線是某二次函數圖象的一部分(如圖),若這個男生出手處A點的坐標為(0,2),鉛球路線的最高處B點的坐標為B(6,5).
(1)求這個二次函數的表達式;
(2)該男生把鉛球推出去多遠?(精確到0.01米).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com