關于x的一元二次方程kx2+2x-1=0有兩個不相等的實數根,則k的取值范圍是 ,若關于x的方程x2-x+cos2α=0有兩個相等的實數根,則銳角α為 ,若方程2x(kx-4)-x2+6=0無實數根,則k的最小整數值為 .
【答案】
分析:先根據關于x的一元二次方程kx
2+2x-1=0有兩個不相等的實數根則k≠0,△>0得到關于k的不等式,求出k的取值范圍;根據關于x的方程x
2-x+cos
2α=0有兩個相等的實數根可知△=0,由△=0及特殊角的三角函數值可求出α的度數;根據方程2x(kx-4)-x
2+6=0無實數根,可得到關于k的不等式,求出k的取值范圍.
解答:解:∵關于x的一元二次方程kx
2+2x-1=0有兩個不相等的實數根,
∴

,解得k>-1且k≠0;
∵關于x的方程x
2-x+cos
2α=0有兩個相等的實數根,
∴△=(-1)
2-4cos
2α=0,解得cosα=±

,
∵α為銳角,
∴cosα=

,
∵cos60°=

,
∴α=60°.
方程2x(kx-4)-x
2+6=0可化為(2k-1)x
2-8x+6=0
∵此方程無實數根,
∴當2k-1=0,即k=

時-8x+6=0,x=

;
當2k-1≠0,即k≠

時,△=64-24(2k-1)<0,解得k>
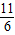
,
∴k的最小整數值為2.
故答案為:k>-1且k≠0;60°;2.
點評:本題考查的是一元二次方程根的判別式及特殊角的三角函數值,熟知一元二次方程根的判別與方程解的關系及特殊角度的三角函數值是解答此題的關鍵.

 ,解得k>-1且k≠0;
,解得k>-1且k≠0; ,
, ,
, ,
, 時-8x+6=0,x=
時-8x+6=0,x= ;
; 時,△=64-24(2k-1)<0,解得k>
時,△=64-24(2k-1)<0,解得k>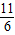 ,
,

 閱讀快車系列答案
閱讀快車系列答案