
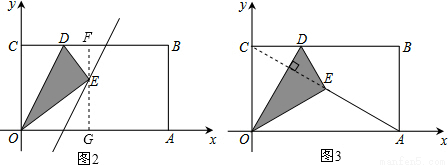
 ,1),在BC邊上選取適當的點D,將△OCD沿OD翻折,點C落在點E處,得到△OED.
,1),在BC邊上選取適當的點D,將△OCD沿OD翻折,點C落在點E處,得到△OED.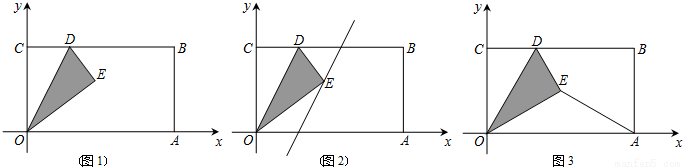
 ,再根據翻折的性質可得OE=OC=1,過點E作EF⊥OA于點F,根據勾股定理求出OF的長度,即可得到點E的坐標;
,再根據翻折的性質可得OE=OC=1,過點E作EF⊥OA于點F,根據勾股定理求出OF的長度,即可得到點E的坐標;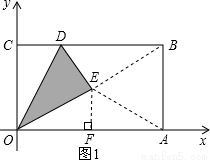 解:(1)∵B(
解:(1)∵B(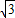 ,1),
,1),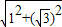 =2,
=2,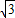 ,1),
,1),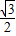 ,
, ),
), ,
, =
=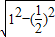 =
=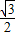 ,
, ,
, ),
), OA=
OA=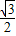 ,
,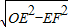 =
=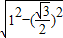 =
= ,
,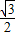 ,
, ),
),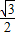 ,
, );
); ,
, ,EG=2×
,EG=2× -1=
-1= ,
, =
= ,
,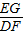 =
=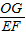 ,
,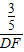 =
=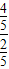 ,
,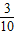 ,
,
 -
-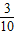 =
= ,
, ,1);
,1);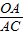 =
=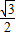 ,
,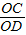 =
=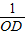 ,
,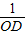 =
=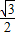 ,
,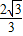 ,
, OD=
OD= ×
×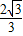 =
=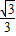 .
.

科目:初中數學 來源: 題型:
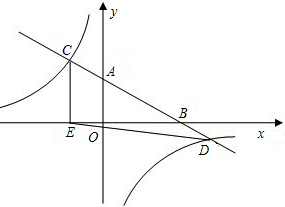 反比例函數的圖象分別交于點C、D,CE⊥x軸于點E,tan∠ABO=
反比例函數的圖象分別交于點C、D,CE⊥x軸于點E,tan∠ABO=| 1 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
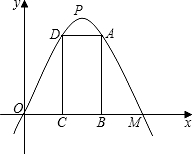 M=4,矩形ABCD的邊BC在線段OM上,點A、D在拋物線上.
M=4,矩形ABCD的邊BC在線段OM上,點A、D在拋物線上.查看答案和解析>>
科目:初中數學 來源: 題型:
 ∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.
∠COA=45°,動點P從點O出發,在梯形OABC的邊上運動,路徑為O→A→B→C,到達點C時停止.作直線CP.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com