
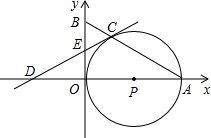
 如圖,點A在x軸的正半軸上,以OA為直徑作⊙P,C是⊙P上一點,過點C的直線y=
如圖,點A在x軸的正半軸上,以OA為直徑作⊙P,C是⊙P上一點,過點C的直線y=
| ||
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
| ||
| 3 |
| 3 |
| OD2+OE2 |
62+(2
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中數學 來源: 題型:
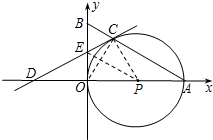
 如圖,點P在y軸的正半軸上,⊙P交x軸于B、C兩點,以AC為直角邊作等腰Rt△ACD,BD分別交y軸和⊙P于E、F兩點,交連接AC、FC.
如圖,點P在y軸的正半軸上,⊙P交x軸于B、C兩點,以AC為直角邊作等腰Rt△ACD,BD分別交y軸和⊙P于E、F兩點,交連接AC、FC.| DE | AO |
查看答案和解析>>
科目:初中數學 來源:2012年福建省福州市中考數學模擬試卷(十)(解析版) 題型:填空題
 ,點B在雙曲線
,點B在雙曲線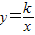 上,點C在直線y=x上,則k的值為 .
上,點C在直線y=x上,則k的值為 .
查看答案和解析>>
科目:初中數學 來源:2011-2012學年浙江省義烏市初中畢業生學業模擬考試數學試卷(解析版) 題型:填空題
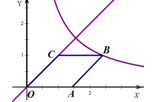
如圖,點A在x軸的正半軸,菱形OABC的面積為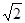 ,點B在雙曲線
,點B在雙曲線 上,點C在直線y=x上,則k的值為____________.
上,點C在直線y=x上,則k的值為____________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com