
【題目】(1)a、b為有理數,且a+b、a﹣b在數軸上如圖所示:
![]()
①判斷:a 0,b 0,a b(用“>”“<”“=”填空).
②若x=|2a+b|﹣3|b|﹣|3﹣2a|+2|b﹣1|,求(2x2-![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )的值;
)的值;
(2)若c為有理數,![]() ,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+
,且ab﹣bc+ac=﹣99,求(3a﹣4b+2c)2+![]() abc的值.
abc的值.
【答案】(1)①<,<,>;②4.5;(2)-378.
【解析】
(1)①由a+b、a﹣b在數軸上的位置判斷a、b的符號以及大小關系;②將x進行化簡,再代入代數式求值;
(2)設![]() =k,代入ab﹣bc+ac=﹣99解出k,然后得到a、b、c的值,再代入求值.
=k,代入ab﹣bc+ac=﹣99解出k,然后得到a、b、c的值,再代入求值.
解:(1)①由a+b、a﹣b在數軸上的位置可知,a+b<﹣3,0<a-b<3,
∵a-b>0,
∴a>b,
∵a+b<﹣3,a-b<3
∴2a<0,即a<0,
∴a<0,b<0,a>b
∴答案為:<,<,>.
②由①可知:a<0,b<0,
∴2a+b<0,3-2a>0,b-1<0,
∴x=|2a+b|﹣3|b|﹣|3﹣2a|+2|b﹣1|
=﹣2a-b+3b﹣3+2a﹣2b+2
=﹣1,
把x=﹣1代入(2x2﹣![]() +3x)﹣4(x﹣x2+
+3x)﹣4(x﹣x2+![]() )的得,
)的得,
原式=(2﹣![]() ﹣3)﹣4(﹣1﹣1+
﹣3)﹣4(﹣1﹣1+![]() )
)
=4.5,
(2)設![]() =k,則a=2k,b=5k,c=7k,
=k,則a=2k,b=5k,c=7k,
∵ab﹣bc+ac=﹣99,
∴10k2﹣35k2+14k2=﹣99,
∴k2=9,
∵a<0,
∴k<0,
∴k=-3
∴a=﹣6,b=﹣15,c=﹣21,
(3a﹣4b+2c)2+![]() abc
abc
=(6k﹣20k+14k)2+![]() abc
abc
=![]() abc
abc
=-378
答:代數式的值為-378.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:
【題目】老師設計了一個數學實驗,給甲、乙、丙三名同學各一張寫有已化為最簡(沒有同類項)的代數式的卡片,規則是兩位同學的代數式相減等于第三位同學的代數式,則實驗成功,甲、乙、丙的卡片如下,丙的卡片有一部分看不清楚了.

(1)計算出甲減乙的結果,并判斷甲減乙能否使實驗成功;
(2)嘉琪發現丙減甲可以使實驗成功,請求出丙的代數式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=x+3與兩坐標軸交于A,B兩點,拋物線y=﹣x2+bx+c過A、B兩點,且交x軸的正半軸于點C.
(1)直接寫出A、B兩點的坐標;
(2)求拋物線的解析式和頂點D的坐標;
(3)在拋物線上是否存在點P,使得△PAB是以AB為直角邊的直角三角形?若存在,求出所有符合條件的點P的坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一條筆直的公路上有![]() 、
、![]() 兩地,甲乙兩人同時出發,甲騎自行車從
兩地,甲乙兩人同時出發,甲騎自行車從![]() 地到
地到![]() 地,乙騎自行車從
地,乙騎自行車從![]() 地到
地到![]() 地,到達
地,到達![]() 地后立即按原路返回
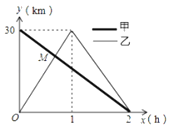
地后立即按原路返回![]() 地.如圖是甲、乙兩人離
地.如圖是甲、乙兩人離![]() 地的距離
地的距離![]() 與行駛時間
與行駛時間![]() 之間的函數圖象,下列說法中①
之間的函數圖象,下列說法中①![]() 、
、![]() 兩地相距30千米;②甲的速度為15千米/時;③點
兩地相距30千米;②甲的速度為15千米/時;③點![]() 的坐標為(
的坐標為(![]() ,20);④當甲、乙兩人相距10千米時,他們的行駛時間是
,20);④當甲、乙兩人相距10千米時,他們的行駛時間是![]() 小時或
小時或![]() 小時. 正確的個數為( )
小時. 正確的個數為( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1:y1=﹣![]() x+b分別與x軸、y軸交于點A、點B,與直線l2:y2=x交于點C(2,2).
x+b分別與x軸、y軸交于點A、點B,與直線l2:y2=x交于點C(2,2).
(1)若y1<y2,請直接寫出x的取值范圍;
(2)點P在直線l1:y1=﹣![]() x+b上,且△OPC的面積為3,求點P的坐標?
x+b上,且△OPC的面積為3,求點P的坐標?

查看答案和解析>>
科目:初中數學 來源: 題型:
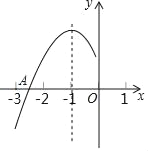
【題目】拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,與x軸的一個交點A在點(﹣3,0)和(﹣2,0)之間,其部分圖象如圖,則下列結論:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④點M(x1,y1)、N(x2,y2)在拋物線上,若x1<x2<﹣1,則y1>y2,⑤abc>0.其中正確結論的個數是( )
A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數學 來源: 題型:
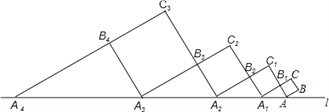
【題目】如圖,正方形ABCB1中,AB=1,AB與直線l的夾角為30°,延長CB1交直線l于點A1,作正方形A1B1C1B2,延長C1B2交直線l于點A2,作正方形A2B2C2B3,延長C2B3交直線l于點A3,作正方形A3B3C3B4,…,依此規律,則A2016A2017=__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學的許多發現都曾位居世界前列,其中“楊輝三角”就是一例.如圖,這個三角形的構造法則:兩腰上的數都是1,其余每個數均為其上方左右兩數之和,它給出了(a+b)n(n為正整數)的展開式(按a的次數由大到小的順序排列)的系數規律.例如,在三角形中第三行的三個數1,2,1,恰好對應(a+b)2=a2+2ab+b2展開式中的系數;第四行的四個數1,3,3,1,恰好對應著(a+b)3=a3+3a2b+3ab2+b2展開式中的系數等等.
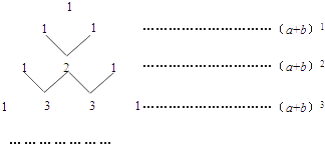
(1)根據上面的規律,則(a+b)5的展開式=________.
(2)利用上面的規律計算:25﹣5×24+10×23﹣10×22+5×2﹣1=________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com