
【題目】某校八年級甲、乙兩班各有學生50人,為了了解這兩個班學生身體素質情況,進行了抽樣調查,過程如下,請補充完整.
(1)收集數據
從甲、乙兩個班各隨機抽取10名學生進行身體素質測試,測試成績(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述數據
按如下分數段整理、描述這兩組樣本數據:

在表中:m= ,n= .
(3)分析數據
①兩組樣本數據的平均數、中位數、眾數如表所示:

在表中:x= ,y= .
②若規定測試成績在80分(含80分)以上的敘述身體素質為優秀,請估計乙班50名學生中身體素質為優秀的學生有 人.
③現從甲班指定的2名學生(1男1女),乙班指定的3名學生(2男1女)中分別抽取1名學生去參加上級部門組織的身體素質測試,用樹狀圖和列表法求抽到的2名同學是1男1女的概率.
【答案】(2)3、2;(3)①75、70;②20;③抽到的2名同學是1男1女的概率為![]() .
.
【解析】(2)由收集的數據即可得;
(3)①根據眾數和中位數的定義求解可得;
②用總人數乘以乙班樣本中優秀人數所占比例可得;
③列表得出所有等可能結果,利用概率公式求解可得.
(2)由收集的數據得知m=3、n=2,
故答案為:3、2;
(3)①甲班成績為:50、60、65、65、75、75、75、80、85、90,
∴甲班成績的中位數x=![]() =75,
=75,
乙班成績70分出現次數最多,所以的眾數y=70,
故答案為:75、70;
②估計乙班50名學生中身體素質為優秀的學生有50×![]() =20人;
=20人;
③列表如下:
男 | 女 | |
男 | 男、男 | 女、男 |
男 | 男、男 | 女、男 |
女 | 男、女 | 女、女 |
由表可知,共有6種等可能結果,其中抽到的2名同學是1男1女的有3種結果,
所以抽到的2名同學是1男1女的概率為![]() .
.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業安徽少年兒童出版社系列答案
暑假作業安徽少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知長方形ABCD中,∠A=∠D=∠B=∠C=90,E是AD上的一點,F是AB上的一點,EF⊥EC,且EF=EC,DE=4cm.

(1)求證:AF=DE.
(2)若AD+DC=18,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校要開展校園文化藝術節活動,為了合理編排節目,對學生最喜愛的歌曲、舞蹈、小品、相聲四類節目進行了一次隨機抽樣調查(每名學生必須選擇且只能選擇一類),并將調查結果繪制成如下不完整統計圖.
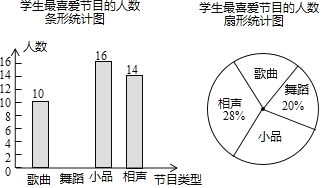
請你根據圖中信息,回答下列問題:
(1)本次共調查了 名學生.
(2)在扇形統計圖中,“歌曲”所在扇形的圓心角等于 度.
(3)補全條形統計圖(標注頻數).
(4)根據以上統計分析,估計該校2000名學生中最喜愛小品的人數為 人.
(5)九年一班和九年二班各有2名學生擅長舞蹈,學校準備從這4名學生中隨機抽取2名學生參加舞蹈節目的編排,那么抽取的2名學生恰好來自同一個班級的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九年三班的小雨同學想了解本校九年級學生對哪門課程感興趣,隨機抽取了部分九年級學生進行調查(每名學生必只能選擇一門課程).將獲得的數據整理繪制如下兩幅不完整的統計圖.
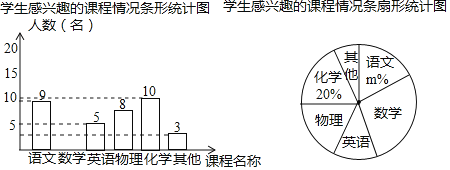
據統計圖提供的信息,解答下列問題:
(1)在這次調查中一共抽取了 名學生,m的值是 .
(2)請根據據以上信息直在答題卡上補全條形統計圖;
(3)扇形統計圖中,“數學”所對應的圓心角度數是 度;
(4)若該校九年級共有1000名學生,根據抽樣調查的結果,請你估計該校九年級學生中有多少名學生對數學感興趣.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代第一部自成體系的數學專著,代表了東方數學的最高成就.它的算法體系至今仍在推動著計算機的發展和應用.書中記載:“今有圓材埋在壁中,不知大小,以鋸鋸之,深一寸,鋸道長一尺,問徑幾何?”譯為:“今有一圓柱形木材,埋在墻壁中,不知其大小,用鋸去鋸這木材,鋸口深1寸(ED=1寸),鋸道長1尺(AB=1尺=10寸)”,問這塊圓形木材的直徑是多少?”
如圖所示,請根據所學知識計算:圓形木材的直徑AC是( )
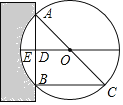
A. 13寸 B. 20寸 C. 26寸 D. 28寸
查看答案和解析>>
科目:初中數學 來源: 題型:
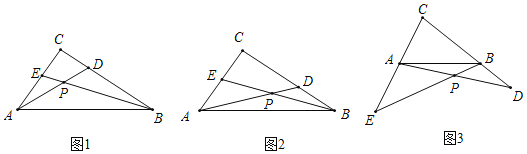
【題目】已知Rt△ABC中,∠ACB=90°,點D、E分別在BC、AC邊上,連結BE、AD交于點P,設AC=kBD,CD=kAE,k為常數,試探究∠APE的度數:
(1)如圖1,若k=1,則∠APE的度數為 ;
(2)如圖2,若k=![]() ,試問(1)中的結論是否成立?若成立,請說明理由;若不成立,求出∠APE的度數.
,試問(1)中的結論是否成立?若成立,請說明理由;若不成立,求出∠APE的度數.
(3)如圖3,若k=![]() ,且D、E分別在CB、CA的延長線上,(2)中的結論是否成立,請說明理由.
,且D、E分別在CB、CA的延長線上,(2)中的結論是否成立,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題7分)如圖,點B、F、C、E在一條直線上,FB=CE,AC=DF,請從下列三個條件:①AB=DE;②∠A=∠D;③∠ACB=∠DFE中選擇一個合適的條件,使AB∥ED成立,并給出證明.

(1)選擇的條件是 (填序號)
(2)證明:
查看答案和解析>>
科目:初中數學 來源: 題型:
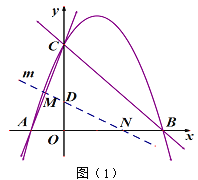
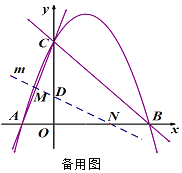
【題目】直線![]() 與x軸、y軸分別交于點B、C,拋物線
與x軸、y軸分別交于點B、C,拋物線![]() 經過點B、C,并與x軸交于另一點A.
經過點B、C,并與x軸交于另一點A.
(1)求此拋物線及直線AC的函數表達式;
(2)垂直于y軸的直線l與拋物線交于點P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),與直線BC交于點,N(
),與直線BC交于點,N(![]() ,
,![]() ),若
),若![]() <
<![]() <
<![]() ,結合函數的圖象,求
,結合函數的圖象,求![]() 的取值范圍;
的取值范圍;
(3)經過點D(0,1)的直線m與射線AC、射線OB分別交于點M、N.當直線m繞點D旋轉時,![]() 是否為定值,若是,求出這個值,若不是,說明理由.
是否為定值,若是,求出這個值,若不是,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,直線AB∥CD,E為AB、CD間的一點,連接EA、EC.
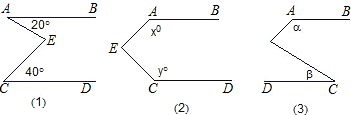
(1)如圖①,若∠A=20°,∠C=40°,則∠AEC= °.
(2)如圖②,若∠A=x°,∠C=y°,則∠AEC= °.
(3)如圖③,若∠A=α,∠C=β,則α,β與∠AEC之間有何等量關系.并簡要說明.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com