【答案】
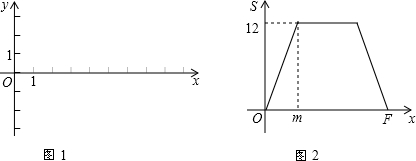
分析:(1)利用當P點運動到A點時,△POC的面積為12,求出斜邊AO即可;
(2)圖1中四邊形ODEF是等腰梯形,點D的坐標為D(m,12),得出y
E=y
D=12,此時圖2中點P運動到與點B重合,利用三角形面積求出OB的長,進而得出B點坐標,以及利用△ABM≌△CON得出C點坐標和利用勾股定理求出FO的長;
(3)根據當點P恰為經過O,B兩點的拋物線的頂點時,當BP為以B,P,Q,R為頂點的菱形的邊時,當BP為以B,P,Q,R為頂點的菱形的對角線時,分別分析得出即可.
解答: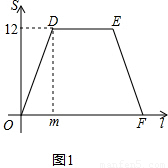
解:(1)根據圖中得出:
當P點運動到A點時,△POC的面積為12,
∴AO=
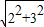
=
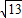
,
∴m=
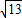
,
故答案為:
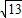
;
(2)∵圖1中四邊形ODEF是等腰梯形,點D的坐標為D(m,12),
∴y
E=y
D=12,此時圖2中點P運動到與點B重合,
∵點B在x軸的正半軸上,
∴S
△BOC=
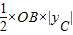
=

×OB×3=12.
解得 OB=8,點B的坐標為(8,0).
此時作AM⊥OB于點M,CN⊥OB于點N.
(如圖2).
∵點C的坐標為C(n,-3),
∴點C在直線y=-3上.
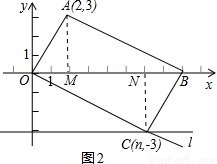
又∵由圖1中四邊形ODEF是等腰梯形可知圖2中的點C在過點O與AB平行的直線l上,
∴點C是直線y=-3與直線l的交點,且∠ABM=∠CON.
又∵|y
A|=|y
C|=3,即AM=CN,
可得△ABM≌△CON.
∴ON=BM=6,點C的坐標為C(6,-3).
∵圖2中 AB=
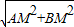
=
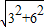
=
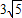
.
∴圖1中DE=
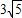
,OF=2x
D+DE=
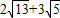
.
(3)①當點P恰為經過O,B兩點的拋物線的頂點時,作PG⊥OB于點G.
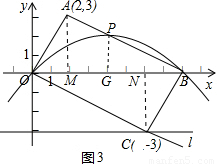
(如圖3)
∵O,B兩點的坐標分別為O(0,0),B(8,0),
∴由拋物線的對稱性可知點P的橫坐標為4,即OG=BG=4.由tan∠ABM=
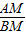
=

=
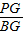
可得PG=2.
∴點P的坐標為P(4,2),
設拋物線W的解析式為y=ax(x-8)(a≠0).
∵拋物線過點P(4,2),
∴4a(4-8)=2.
解得 a=
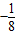
.
∴拋物線W的解析式為y=
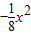
+x.
②如圖4.
i)當BP為以B,P,Q,R為頂點的菱形的邊時,
∵點Q在直線y=-1上方的拋物線W 上,點P為拋物線W的頂點,
結合拋物線的對稱性可知點Q只有一種情況,點Q與原點重合,其坐標為Q
1(0,0).
ii)當BP為以B,P,Q,R為頂點的菱形的對角線時,可知BP的中點的坐標為(6,1),BP的中垂線的解析式為y=2x-11.
∴點Q
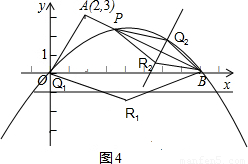
2的橫坐標是方程
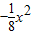
+x=2x-11的解.
將該方程整理得 x
2+8x-88=0.
解得x=-4±
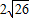
.
由點Q在直線y=-1上方的拋物線W上,結合圖4可知點Q
2的橫坐標為
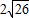
-4.
∴點Q
2的坐標是Q
2(
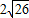
-4,
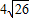
-19).
綜上所述,符合題意的點Q的坐標是Q
1(0,0),Q
2(
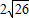
-4,
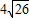
-19).
點評:此題主要考查了二次函數的綜合應用以及菱形性質和等腰梯形性質等知識,根據數形結合得出梯形面積進而得出B,C點的坐標是解題關鍵.

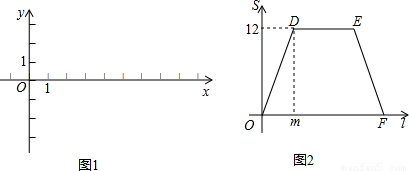
 解:(1)根據圖中得出:
解:(1)根據圖中得出: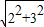 =
=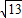 ,
,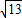 ,
,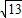 ;
;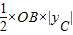 =
= ×OB×3=12.
×OB×3=12.
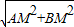 =
=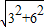 =
=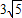 .
.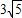 ,OF=2xD+DE=
,OF=2xD+DE=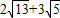 .
.  (如圖3)
(如圖3)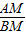 =
= =
=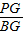 可得PG=2.
可得PG=2.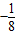 .
.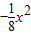 +x.
+x. ②如圖4.
②如圖4.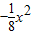 +x=2x-11的解.
+x=2x-11的解.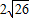 .
.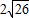 -4.
-4.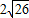 -4,
-4,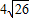 -19).
-19). 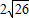 -4,
-4,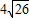 -19).
-19).

 同步奧數系列答案
同步奧數系列答案