
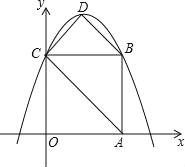
【題目】如圖,在平面直角坐標系中,正方形OABC的邊長為4,頂點A、C分別在x軸、y軸的正半軸,拋物線y=-![]() x2+bx+c經過B、C兩點,點D為拋物線的頂點,連接AC、BD、CD.
x2+bx+c經過B、C兩點,點D為拋物線的頂點,連接AC、BD、CD.
(1)求此拋物線的解析式.
(2)求此拋物線頂點D的坐標和四邊形ABCD的面積.
 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
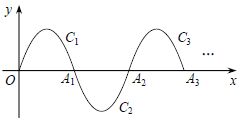
【題目】如圖,一段拋物線![]() ,記為C1,它與
,記為C1,它與![]() 軸交于點O,A1;將C1繞點A1旋轉180°得C2,交
軸交于點O,A1;將C1繞點A1旋轉180°得C2,交![]() 軸于點A2;將C2繞點A2旋轉180°得C3,交
軸于點A2;將C2繞點A2旋轉180°得C3,交![]() 軸于點A3;……如此進行下去,得到一“波浪線”.若點P(41,
軸于點A3;……如此進行下去,得到一“波浪線”.若點P(41,![]() )在此“波浪線”上,則
)在此“波浪線”上,則![]() 的值為
的值為
A.2 B.![]() C.0 D.
C.0 D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 兩邊及其中一邊的對角分別相等的兩個三角形全等
B. 三角形的外角等于它的兩個內角的和
C. 斜邊和一條直角邊相等的兩個直角三角形全等
D. 兩條直線被第三條直線所截,內錯角相等
查看答案和解析>>
科目:初中數學 來源: 題型:
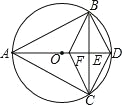
【題目】如圖,已知△ABC內接于⊙O,且AB=AC,直徑AD交BC于點E,F是OE上的一點,使CF∥BD.
(1)求證:BE=CE;
(2)試判斷四邊形BFCD的形狀,并說明理由;
(3)若BC=8,AD=10,求CD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列敘述:①延長直線AB到C;②延長射線AB到C;③延長線段AB到C;④反向延長線段BA到C;⑤反向延長射線AB到C其中正確的有_________(填序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四邊形ABCD中,AB=BC=CD=DA,如果添加一個條件,即可推出該四邊形是正方形,那么這個條件可以是( )
A. AC⊥BD B. AB∥CD C. ∠A=90° D. ∠A=∠C
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com