
【題目】如圖1,長方形ABCD中,AB=CD=7cm,AD=BC=5cm,∠A=∠B=∠C=∠D=90°,點E在線段AB上以lcms的速度由點A向點B運動,與此同時點F在線段BC上由點B向點C運動,設運動的時間均為ts.
(1)若點F的運動速度與點E的運動速度相等,當t=2時:
①判斷△BEF與△ADE是否全等?并說明理由;
②求∠EDF的度數.
(2)如圖2,將圖1中的“長方形ABCD”改為“梯形ABCD”,且∠A=∠B=70°,AB=7cm,AD=BC=5cm,其他條件不變.設點F的運動速度為xcm/s.是否存在x的值,使得△BEF與△ADE全等?若存在,直接寫出相應的x及t的值;若不存在,請說明理由.

【答案】(1)①△BEF≌△ADE;②由①得DE=EF,∠BEF=∠ADE;(2)存在,①如圖2,當△DAE≌△EBF時,x=1,t=2;②如圖3,當△ADE≌△BFE時,AE=BE,AD=BF,x=![]() ,t=
,t=![]() .
.
【解析】
![]() 根據SAS證明:
根據SAS證明:![]() ≌
≌![]() ;
;![]() 由
由![]() :
:![]() ≌
≌![]() 得
得![]() ,
,![]() ,證明
,證明![]() 是等腰直角三角形可得結論;
是等腰直角三角形可得結論;![]() 分兩種情況:
分兩種情況:![]() 如圖2,當
如圖2,當![]() ≌
≌![]() 時,
時,![]() 如圖3,當
如圖3,當![]() ≌
≌![]() 時,分別根據
時,分別根據![]() ,
,![]() ,列方程組可得結論.
,列方程組可得結論.
解:(1)①△BEF≌△ADE,理由如:
當t=2時,AE=BF=2,
∴BE=AB-AD=7-2=5,
∵AD=5,
∴BE=AD,
∵∠A=∠B=90°,
∴△BEF≌△ADE;
②由①得DE=EF,∠BEF=∠ADE,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠BEF+∠AED=90°,
∴∠DEF=180°-(∠BEF+∠AED)=90°,
∵DE=EF
∴∠EDF=∠EFD,
∵∠EDF+∠EFD=90°,
∴∠EDF=45°;
(2)存在,
①如圖2,當△DAE≌△EBF時,
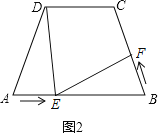
∴AD=BE,AE=BF,
則![]()
∴x=1,t=2;
②如圖3,當△ADE≌△BFE時,AE=BE,AD=BF,
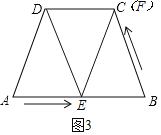
則![]() ,
,
∴x=![]() ,t=
,t=![]() .
.


 捷徑訓練檢測卷系列答案
捷徑訓練檢測卷系列答案 小夫子全能檢測系列答案
小夫子全能檢測系列答案科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD的對角線AC、BD相較于點O,EF過點O,且與AD、BC分別相交于E、F,若AB=4,BC=5,OE=1.5,則四邊形EFCD的周長是( )

A.16B.14C.12D.10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有A,B兩個黑布袋,A布袋中有兩個完全相同的小球,分別標有數字1和2.B 布袋中有三個完全相同的小球,分別標有數字﹣1,﹣2和﹣3.小明從A布袋中隨機取出一個小球,記錄其標有的數字為x,再從B布袋中隨機取出一個小球,記錄其標有的數字為y,這樣就確定點Q的一個坐標為(x,y).
(1)用列表或畫樹狀圖的方法寫出點Q的所有可能坐標;
(2)求點Q落在直線y=﹣x﹣1上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
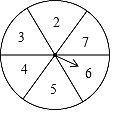
【題目】如圖,現有一個轉盤被平均分成6等份,分別標有數字2、3、4、5、6、7這六個數字,轉動轉盤,當轉盤停止時,指針指向的數字即為轉出的數字,求:
(1)轉到數字10是______(從“不確定事件”“必然事件”“不可能事件”選一個填入);
(2)轉動轉盤,轉出的數字大于3的概率是______;
(3)現有兩張分別寫有3和4的卡片,要隨機轉動轉盤,轉盤停止后記下轉出的數字,與兩張卡片上的數字分別作為三條線段的長度.
①這三條線段能構成三角形的概率是多少?
②這三條線段能構成等腰三角形的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】龍人文教用品商店欲購進![]() 、
、![]() 兩種筆記本,用160元購進的
兩種筆記本,用160元購進的![]() 種筆記本與用240元購進的
種筆記本與用240元購進的![]() 種筆記本數量相同,每本
種筆記本數量相同,每本![]() 種筆記本的進價比每本
種筆記本的進價比每本![]() 種筆記本的進價貴10元.
種筆記本的進價貴10元.
(1)求![]() 、
、![]() 兩種筆記本每本的進價分別為多少元?
兩種筆記本每本的進價分別為多少元?
(2)若該商店準備購進![]() 、
、![]() 兩種筆記本共100本,且購買這兩種筆記本的總價不超過2650元,則至少購進
兩種筆記本共100本,且購買這兩種筆記本的總價不超過2650元,則至少購進![]() 種筆記本多少本?
種筆記本多少本?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某汽車制造廠開發一款新式電動汽車,計劃一年生產安裝![]() 輛.由于抽調不出足夠的熟練工來完成新式電動汽車的安裝,工廠決定招聘一些新工人.他們經過培訓后上崗,也能獨立進行電動汽車的安裝.生產開始后,調研部門發現:
輛.由于抽調不出足夠的熟練工來完成新式電動汽車的安裝,工廠決定招聘一些新工人.他們經過培訓后上崗,也能獨立進行電動汽車的安裝.生產開始后,調研部門發現:![]() 名熟練工和
名熟練工和![]() 名新工人每月可安裝
名新工人每月可安裝![]() 輛電動汽車;
輛電動汽車;![]() 名熟練工和
名熟練工和![]() 名新工人每月可安裝
名新工人每月可安裝![]() 輛電動汽車.
輛電動汽車.
(1)每名熟練工和新工人每月分別可以安裝多少輛電動汽車?
(2)如果工廠招聘![]() 名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一年的安裝任務,那么工廠有哪幾種新工人的招聘方案?
名新工人,使得招聘的新工人和抽調的熟練工剛好能完成一年的安裝任務,那么工廠有哪幾種新工人的招聘方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,∠A![]() ,P是BC邊上的一點,
,P是BC邊上的一點,![]() ,
,![]() 是點P關于AB、AC的對稱點,連結
是點P關于AB、AC的對稱點,連結![]() ,分別交AB、AC于點D、E.
,分別交AB、AC于點D、E.
①若![]() ,求
,求![]() 的度數;
的度數;
②請直接寫出∠A與![]() 的數量關系:___________________________;
的數量關系:___________________________;
(2)如圖2,在△ABC中,若∠BAC![]() ,用三角板作出點P關于AB、AC的對稱點
,用三角板作出點P關于AB、AC的對稱點![]() 、
、![]() ,(不寫作法,保留作圖痕跡),試判斷點
,(不寫作法,保留作圖痕跡),試判斷點![]() ,
,![]() 與點A是否在同一直線上,并說明理由.
與點A是否在同一直線上,并說明理由.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,若拋物線L1的頂點A在拋物線L2上,拋物線L2的頂點B也在拋物線L1上(點A與點B不重合),我們定義:這樣的兩條拋物L1,L2互為“友好”拋物線,可見一條拋物線的“友好”拋物線可以有多條.
(1)如圖2,已知拋物線L3:y=2x2-8x+4與y軸交于點C,試求出點C關于該拋物線對稱軸對稱的點D的坐標;
(2)請求出以點D為頂點的L3的友好拋物線L4的解析式,并指出L3與L4中y同時隨x增大而增大的自變量的取值范圍;
(3)若拋物y=a1 (x-m) 2+n的任意一條友好拋物線的解析式為y=a2 (x-h) 2+k,請寫出a1與a2的關系式,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com