解:要使
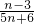
可約分,不妨設分子與分母有公因數a,
顯然應用a>1,并且設分子:n-13=ak
1,①
分母:5n+6=ak
2.②
其中k
1,k
2為自然數.
由①得n=13+ak
1,將之代入②得
5(13+ak
1)+6=ak
2,
即71+5ak
1=ak
2,
所以a(k
2-5k
1)=71.
由于71是質數,且a>1,所以a=71,所以
n=k
1•71+13.
故n最小為84.
分析:要使
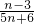
可約分,分子與分母有公因數,設分子:n-13=ak
1,①;分母:5n+6=ak
2,②;整理得到n=k
1•71+13.從而求得n的最小值.
點評:本題考查了約分,找到分子與分母的最大公約數是解此題的關鍵.

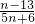 為可約分數,則自然數n的最小值應是多少?
為可約分數,則自然數n的最小值應是多少?