
|

|


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
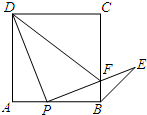 如圖,動點P是正方形ABCD邊AB上運動(不與點A、B重合),連接PD并將線段PD繞點P順時針方向旋轉90°得到線段PE,PE交邊BC于點F,連接BE、DF.
如圖,動點P是正方形ABCD邊AB上運動(不與點A、B重合),連接PD并將線段PD繞點P順時針方向旋轉90°得到線段PE,PE交邊BC于點F,連接BE、DF.| AP | AB |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源:2011年初中畢業升學考試(江蘇無錫卷)數學 題型:解答題
如圖9,點P是正方形ABCD邊AB上一點(不與點A.B重合),連接PD并將線段PD繞點P順時針方向旋轉90°得到線段PE, PE交邊BC于點F.連接BE、DF。
(1)求證:∠ADP=∠EPB;
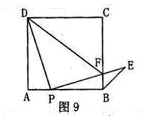 (2)求∠CBE的度數;
(2)求∠CBE的度數;
(3)當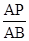 的值等于多少時.△PFD∽△BFP?并說明理由.
的值等于多少時.△PFD∽△BFP?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com