解:(1)設三邊為a,b,c,
∵斜邊上中線為2,
∴c=4
且
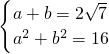
?
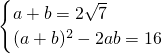
?
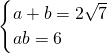
,
∴S
△ABC=3,
(2)設內切圓半徑為r,則
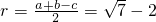
,
∴
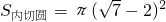
,
(3)tgA•tgB=1,
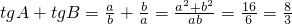
,
∴一元二次方程為
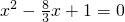
,
即3x
2-8x+3=0.
分析:(1)首先根據直角三角形的性質:斜邊上的中線等于斜邊的一半,可得到c=4,再根據已知條件得到關于a,b的方程組,可解出ab=6,進而可得到直角三角形的面積.
(2)由(1)可解得a+b=2

,則內切圓半徑=

,求出半徑后再用圓的面積公式S=πr
2,求出直角三角形內切圓的面積;
(3)根據條件直角三角形兩個銳角的正切tgA和tgB是一個一元二次方程的兩個根,求出tgA•tgB與tgA+tgB,再根據根與系數的關系寫出方程即可.
點評:此題主要考查了直角三角形的性質,根與系數的關系,三角形的內切圓與圓心,以及三角函數的應用,準確把握每個知識點是解題的關鍵,很多同學由于基礎知識掌握不好導致錯誤的出現.

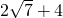 ,斜邊上中線為2.
,斜邊上中線為2.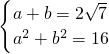 ?
?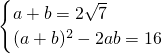 ?
?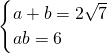 ,
,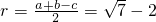 ,
,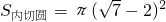 ,
,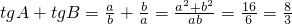 ,
,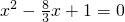 ,
, ,則內切圓半徑=
,則內切圓半徑= ,求出半徑后再用圓的面積公式S=πr2,求出直角三角形內切圓的面積;
,求出半徑后再用圓的面積公式S=πr2,求出直角三角形內切圓的面積;
