
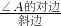 ,cosA=
,cosA=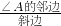 ,tanA=
,tanA= ,cotA=
,cotA=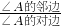
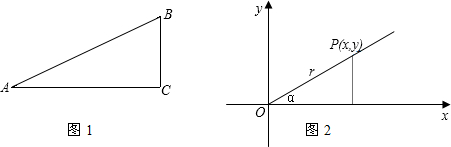
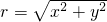 (r總是正的),然后把角α的三角函數(shù)規(guī)定為:
(r總是正的),然后把角α的三角函數(shù)規(guī)定為: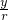 ,cosα=
,cosα=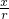 ,tanα=
,tanα= ,cotα=
,cotα=
 ),且cosα=
),且cosα=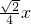 ,則tanα______;
,則tanα______; ,cosα=
,cosα= 或sinα=-
或sinα=- ,cosα=-
,cosα=- .
. 或sinα+cosα=-
或sinα+cosα=- .
.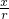 =
=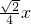 ,則r=2
,則r=2 ,
, ,
, =-
=-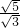 =-
=- .
. ,
,
 ]
] ,-
,- ,[1,
,[1, ].
].

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
 學(xué)習(xí)過三角函數(shù),我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉(zhuǎn)化.
學(xué)習(xí)過三角函數(shù),我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉(zhuǎn)化.| 底邊 |
| 腰 |
| BC |
| AB |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
| • |
| 3 |
| • |
| 2 |
| • |
| 3 |
| • |
| 2 |
| • |
| 3 |
| • |
| 2 |
| 32 |
| 99 |
| • |
| 3 |
| • |
| 2 |
| 32 |
| 99 |
| • |
| 3 |
| • |
| 8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
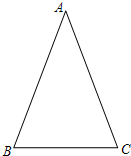
 學(xué)習(xí)過三角函數(shù),我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉(zhuǎn)化.類似的,也可以在等腰三角形中建立邊角之間的聯(lián)系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A=
學(xué)習(xí)過三角函數(shù),我們知道在直角三角形中,一個銳角的大小與兩條邊長的比值相互唯一確定,因此邊長與角的大小之間可以相互轉(zhuǎn)化.類似的,也可以在等腰三角形中建立邊角之間的聯(lián)系,我們定義:等腰三角形中底邊與腰的比叫做頂角的正對(sad).如圖,在△ABC中,AB=AC,頂角A的正對記作sadA,這時sad A=| 1 |
| 2 |
| 2 |
| 2 |
| 3 |
| 3 |
| 3 |
| 5 |
2-2
|
2-2
|
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
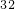 可化成0.323232….如果我們要把0.
可化成0.323232….如果我們要把0.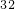 化成分?jǐn)?shù),可以用以下方法進(jìn)行:設(shè)x=0.
化成分?jǐn)?shù),可以用以下方法進(jìn)行:設(shè)x=0.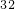 ,即x=0.323232…,兩邊同乘以100,得100x=32.323232…,即100x=32+0.323232…,所以100x=32+x.解這個方程得:x=
,即x=0.323232…,兩邊同乘以100,得100x=32.323232…,即100x=32+0.323232…,所以100x=32+x.解這個方程得:x=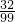 ,即0.
,即0.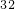 =
=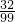 .試用上面的方法把0.
.試用上面的方法把0.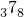 化成分?jǐn)?shù).
化成分?jǐn)?shù).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com