【題目】在哈市地鐵一號線施工建設中，安排甲、乙兩個工程隊完成大連北路至新疆大街路段的鐵軌鋪設任務，該路段全長3600米．已知甲隊每天鋪設鐵軌的米數是乙隊每天鋪設鐵軌米數的1.5倍，并且甲、乙兩隊分別單獨完成600米長度路段時，甲隊比乙隊少用10天．
（1）求甲、乙兩個工程隊每天各能鋪設鐵軌多少米？
（2）若甲隊每天施工的費用為4萬元，乙隊每天施工的費用為3萬元，要使甲、乙兩隊合作完成大連北路至新疆大街全長3600米的總費用不超過520萬元，則至少應安排甲隊施工多少天？
百分學生作業本題練王系列答案科目：初中數學 來源： 題型：
【題目】閱讀下列材料，然后解決問題：和、差、倍、分等問題中有著廣泛的應用，截長法與補短法在證明線段的和、差、倍、分等問題中有著廣泛的應用．具體的做法是在某條線段上截取一條線段等于某特定線段，或將某條線段延長，使之與某特定線段相等，再利用全等三角形的性質等有關知識來解決數學問題．
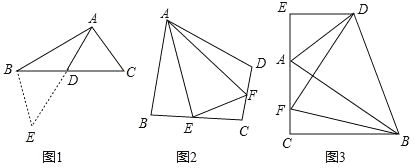
（1）如圖1，在△ABC中，若 AB＝12，AC＝8，求 BC邊上的中線AD的取值范圍．
解決此問題可以用如下方法：延長AD到點E使 DE＝AD，再連接 BE，把AB、AC、2AD集中在△ABE中．利用三角形三邊的關系即可判斷中線 AD的取值范圍是_______.
問題解決：
（2）如圖2，在四邊形ABCD中，AB＝AD，∠ABC+∠ADC＝180°，E、F分別是邊BC，CD上的兩點，且∠EAF＝
∠BAD，求證：BE+DF＝EF．
問題拓展：
（3）如圖3，在△ABC中，∠ACB＝90°，∠CAB＝60°，點D是△ABC 外角平分線上一點，DE⊥AC交 CA延長線于點E，F是 AC上一點，且DF＝DB．
求證：AC﹣AE＝AF．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】張明和李強兩名運動愛好者周末相約到東湖綠道進行跑步鍛煉．（1）周日早上6點，張明和李強同時從家出發，分別騎自行車和步行到離家距離分別為4.5千米和1.2千米的綠道落雁島入口匯合，結果同時到達，且張明每分鐘比李強每分鐘多行220米，求張明和李強的速度分別是多少米/分？
（1）兩人到達綠道后約定先跑 6 千米再休息，李強的跑步速度是張明跑步速度的m倍，兩人在同起點，同時出發，結果李強先到目的地n分鐘．
①當m＝12，n＝5時，求李強跑了多少分鐘？
②張明的跑步速度為 米/分（直接用含m，n的式子表示）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】將一副三角板按如圖放置，則下列結論：
①如果∠2=30°，則有AC∥DE；
②∠BAE+∠CAD =180°；
③如果BC∥AD，則有∠2=45°；
④如果∠CAD=150°，必有∠4=∠C；
正確的有( )
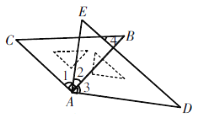
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】隨著“足球進校園”工作的推進，全國中小學生的身體素質普遍增強．某校為了準確把握學生在“足球進校園”活動開展后的體質情況，從全校學生中隨機抽取部分學生進行身體素質測試，測試的結果分為A、B、C、D、E五個等級，并根據樣本繪制了兩幅統計圖，請根據統計圖的信息回答下列問題：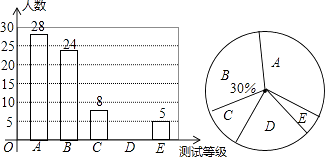 
（1）本次抽樣調查基抽取了學生多少人？
（2）在本次被調查的學生中，求測試結果為D等級的學生人數，并補全條形統計圖．
（3）若該學校共有學生1200人，請你根據抽樣調查的結果估計該學校全體學生中身體素質測試結果為A等級的學生有多少人？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】“綠色出行，低碳健身”已成為廣大市民的共識．為方便市民出行，東臺市推出了公共自行車系統，收費以小時為單位，每次使用不超過1小時的免費，超過1小時后，不足1小時的部分按1小時收費．小紅同學通過調查得知，自行車使用時間為3小時，收費2元；使用時間為4小時，收費3元．她發現當使用時間超過1小時后用車費用與使用時間之間存在一次函數的關系．
（1）設使用自行車的費用為
元，使用時間為
小時（為大于1的整數），求與的函數解析式；
（2）若小紅此次使用公共自行車5小時，則她應付多少元費用？
（3）若小紅此次使用公共自行車付費6元，求她所使用自行車的時間．
查看答案和解析>>
科目：初中數學 來源： 題型：
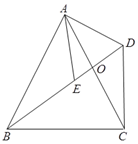
【題目】如圖，四邊形ABCD中，對角線AC、BD交于點O，AB＝AC，點E是BD上一點，且AE＝AD，∠EAD＝∠BAC．
⑴ 求證：∠ABD＝∠ACD；
⑵ 若∠ACB＝65°，求∠BDC的度數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
