
【題目】如圖,以AD為直徑的半圓O經過Rt△ABC斜邊AB的兩個端點,交直角邊AC于點E,B、E是半圓弧的三等分點,弧BE的長為![]() π,則圖中陰影部分的面積為( )
π,則圖中陰影部分的面積為( )
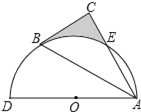
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABE中,∠B=90°,AB=BE,將△ABE繞點A逆時針旋轉45°,得到△AHD,過D作DC⊥BE交BE的延長線于點C,連接BH并延長交DC于點F,連接DE交BF于點O.下列結論:①DE平分∠HDC;②DO=OE;③H是BF的中點;④BC-CF=2CE;⑤CD=HF,其中正確的有( )
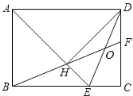
A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx+c(a≠0)與y軸交于點C,與x軸交于A,B兩點,其中點B的坐標為B(4,0),拋物線的對稱軸交x軸于點D,CE∥AB,并與拋物線的對稱軸交于點E.現有下列結論:①a>0;②b>0;③4a+2b+c<0;④AD+CE=4.其中所有正確結論的序號是( )
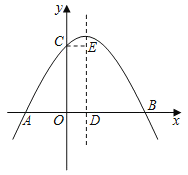
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線交x軸于A,B兩點(A在B右邊),A(3,0),B(1,0)交y軸于C點,C(0,3),連接AC;
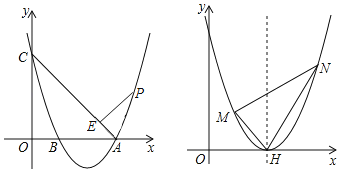
(1)求拋物線的解析式;
(2)P為拋物線上的一點,作PE⊥CA于E點,且CE=3PE,求P點坐標;
(3)將原拋物線向上平移1個單位拋物線的對稱軸交x軸于H點,過H作直線MH,NH,當MH⊥NH時,求MN恒過的定點坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
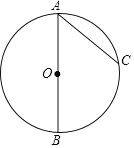
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,連接AC.過點B作⊙O的切線,交AC的延長線于點D,在AD上取一點E,使AE=AB,連接BE,交⊙O于點F.
請補全圖形并解決下面的問題:
(1)求證:∠BAE=2∠EBD;
(2)如果AB=5,sin∠EBD=![]() .求BD的長.
.求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】身高1.65米的兵兵在建筑物前放風箏,風箏不小心掛在了樹上.在如圖所示的平面圖形中,矩形CDEF代表建筑物,兵兵位于建筑物前點B處,風箏掛在建筑物上方的樹枝點G處(點G在FE的延長線上).經測量,兵兵與建筑物的距離BC=5米,建筑物底部寬FC=7米,風箏所在點G與建筑物頂點D及風箏線在手中的點A在同一條直線上,點A距地面的高度AB=1.4米,風箏線與水平線夾角為37°.
(1)求風箏距地面的高度GF;
(2)在建筑物后面有長5米的梯子MN,梯腳M在距墻3米處固定擺放,通過計算說明:若兵兵充分利用梯子和一根米長的竹竿能否觸到掛在樹上的風箏?
(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中數學 來源: 題型:
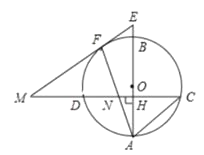
【題目】如圖,已知AB是圓O的直徑,弦CD⊥AB,垂足為H,在CD上有點N滿足CN=CA,AN交圓O于點F,過點F的AC的平行線交CD的延長線于點M,交AB的延長線于點E.
(1)求證:EM是圓O的切線;
(2)若AC:CD=5:8,AN=3![]() ,求圓O的直徑長度.
,求圓O的直徑長度.
(3)在(2)的條件下,直接寫出FN的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,AB⊥x軸,垂足為A.反比例函數y=![]() (x>0)的圖象經過點C,交AB于點D.已知AB=4,BC=
(x>0)的圖象經過點C,交AB于點D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)連接OC,若BD=BC,求OC的長.
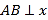
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com