
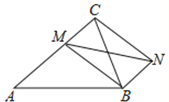
【題目】如圖,已知在△ABC中,AB=AC=13,BC=10,點M是AC邊上任意一點,連接MB,以MB、MC為鄰邊作平行四邊形MCNB,連接MN,則MN的最小值是______
【答案】![]()
【解析】
設MN與BC交于點O,連接AO,過點O作OH⊥AC于H點,根據等腰三角形的性質和勾股定理可求AO和OH長,若MN最小,則MO最小即可,而O點到AC的最短距離為OH長,所以MN最小值是2OH.
解:設MN與BC交于點O,連接AO,過點O作OH⊥AC于H點,
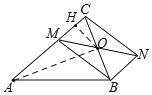
∵四邊形MCNB是平行四邊形,
∴O為BC中點,MN=2MO.
∵AB=AC=13,BC=10,
∴AO⊥BC.
在Rt△AOC中,利用勾股定理可得
AO=![]() =12.
=12.
利用面積法:AO×CO=AC×OH,
即12×5=13×OH,解得OH=![]() .
.
當MO最小時,則MN就最小,O點到AC的最短距離為OH長,
所以當M點與H點重合時,MO最小值為OH長是![]() .
.
所以此時MN最小值為2OH=![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx﹣5的圖象與x軸交于A、B兩點,與y軸交于點C,其中點A坐標為(﹣1,0),一次函數y=x+k的圖象經過點B、C.
(1)試求二次函數及一次函數的解析式;
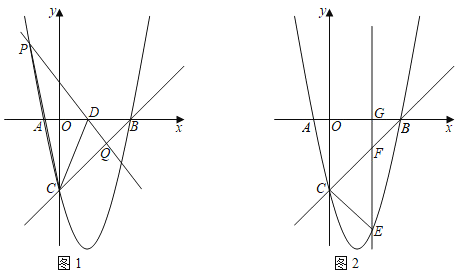
(2)如圖1,點D(2,0)為x軸上一點,P為拋物線上的動點,過點P、D作直線PD交線段CB于點Q,連接PC、DC,若S△CPD=3S△CQD,求點P的坐標;
(3)如圖2,點E為拋物線位于直線BC下方圖象上的一個動點,過點E作直線EG⊥x軸于點G,交直線BC于點F,當EF+![]() CF的值最大時,求點E的坐標.
CF的值最大時,求點E的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個草莓采摘園為吸引顧客,在草莓銷售價格相同的基礎上分別推出優惠方案,甲園:顧客進園需購買門票,采摘的草莓按六折優惠.乙園:顧客進園免門票,采摘草莓超過一定數量后,超過的部分打折銷售.活動期間,某顧客的草莓采摘量為x kg,若在甲園采摘需總費用y1元,若在乙園采摘需總費用y2元, y1,y2與x之間的函數圖象如圖所示,則下列說法中錯誤的是( )
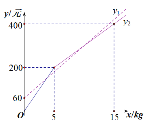
A.甲園的門票費用是60元
B.草莓優惠前的銷售價格是40元/kg
C.乙園超過5 kg后,超過的部分價格優惠是打五折
D.若顧客采摘12 kg草莓,那么到甲園或乙園的總費用相同
查看答案和解析>>
科目:初中數學 來源: 題型:
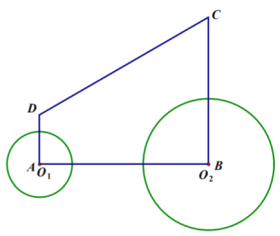
【題目】如圖,直角梯形![]() 中,
中,![]() 的圓心
的圓心![]() 從點
從點![]() 開始沿折線
開始沿折線![]() 以
以![]() 的速度向點
的速度向點![]() 運動,
運動,![]() 的圓心
的圓心![]() 從點
從點![]() 開始沿
開始沿![]() 邊以
邊以![]()
![]() 的速度向點
的速度向點![]() 運動,
運動,![]() 半徑為
半徑為![]() 的半徑為
的半徑為![]() ,若
,若![]() 分別從點
分別從點![]() 、點
、點![]() 同時出發,運動的時間為
同時出發,運動的時間為![]()
(1)請求出![]() 與腰
與腰![]() 相切時
相切時![]() 的值;
的值;
(2)在![]() 范圍內,當
范圍內,當![]() 為何值時,
為何值時,![]() 與
與![]() 外切?
外切?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與x軸交于A(-1,0)和B(3,0)兩點,與y軸交于點C,對稱軸與x軸交于點E,點D為頂點,連接BD、CD、BC.
與x軸交于A(-1,0)和B(3,0)兩點,與y軸交于點C,對稱軸與x軸交于點E,點D為頂點,連接BD、CD、BC.

(1)求證△BCD是直角三角形;
(2)點P為線段BD上一點,若∠PCO+∠CDB=180°,求點P的坐標;
(3)點M為拋物線上一點,作MN⊥CD,交直線CD于點N,若∠CMN=∠BDE,請直接寫出所有符合條件的點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
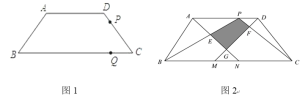
(1)梯形ABCD的面積等于 .
(2)如圖1,動點P從D點出發沿DC以DC以每秒1個單位的速度向終點C運動,動點Q從C點出發沿CB以每秒2個單位的速度向B點運動.兩點同時出發,當P點到達C點時,Q點隨之停止運動.當PQ∥AB時,P點離開D點多少時間?
(3)如圖2,點K是線段AD上的點,M、N為邊BC上的點,BM=CN=5,連接AN、DM,分別交BK、CK于點E、F,記△ ADG和△ BKC重疊部分的面積為S,求S的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,以
中,以![]() 為直徑的
為直徑的![]() ,交
,交![]() 于點
于點![]() ,且
,且![]() 交直線
交直線![]() 于點
于點![]() ,連接
,連接![]() .
.
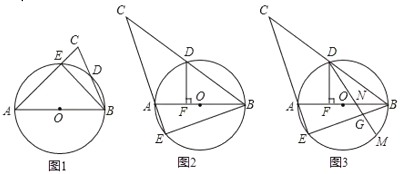
![]() 如圖1,求證:
如圖1,求證:![]() ;
;
![]() 如圖2,
如圖2,![]() 為鈍角時,過點
為鈍角時,過點![]() 作
作![]() 于點
于點![]() 求證:
求證:![]() ;
;
![]() 如圖3,在
如圖3,在![]() 的條件下,在∠BDF的內部作
的條件下,在∠BDF的內部作![]() ,使
,使![]() 分別交
分別交![]() 于點
于點![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
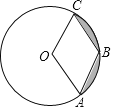
【題目】如圖,已知⊙O的半徑是2,點A、B、C在⊙O上,若四邊形OABC為菱形,則圖中陰影部分面積為( )
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學初三年級積極推進走班制教學.為了了解一段時間以來,“至善班”的學習效 果,年級組織了多次定時測試,現隨機選取甲、乙兩個“至善班”,從中各抽取![]() 名同學在某一次定時測試中的數學成績,其結果記錄如下:
名同學在某一次定時測試中的數學成績,其結果記錄如下:
收集數據:
“至善班”甲班![]() 的名同學的數學成績統計(滿分為 100 分)(單位:分)
的名同學的數學成績統計(滿分為 100 分)(單位:分)
![]()
![]()
“至善班”乙班的![]() 名同學的數學成績統計(滿分為 100 分)(單位:分)
名同學的數學成績統計(滿分為 100 分)(單位:分)
![]()
![]()
整理數據:(成績得分用![]() 表示)
表示)
分數 數量 班級 |
|
|
|
|
|
甲班(人數) | 1 | 3 | 4 | 6 | 6 |
乙班(人數) | 1 | 1 | 8 | 6 | 4 |
分析數據,并回答下列問題:
![]() 完成下表:
完成下表:
平均數 | 中位數 | 眾數 | |
甲班 |
|
|
|
乙班 |
|
|
|
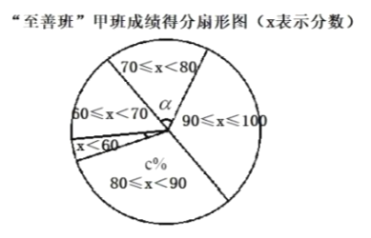
![]() 在“至善班”甲班的扇形圖中, 成績在
在“至善班”甲班的扇形圖中, 成績在![]() 的扇形中,所對的圓心角
的扇形中,所對的圓心角![]() 的度數為 . 估計全部“至善班”的
的度數為 . 估計全部“至善班”的![]() 人中優秀人數為 人.(
人中優秀人數為 人.(![]() 分及以上為優秀).
分及以上為優秀).
![]() 根據以上數據,你認為“至善班” 班(填“甲”或“乙”)所選取做樣本 的同學的學習效果更好一些,你所做判斷的理由是:
根據以上數據,你認為“至善班” 班(填“甲”或“乙”)所選取做樣本 的同學的學習效果更好一些,你所做判斷的理由是:
①
②
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com