
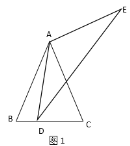
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 邊上一動點(diǎn),以點(diǎn)
邊上一動點(diǎn),以點(diǎn)![]() 為頂點(diǎn),
為頂點(diǎn),![]() 為一腰作等腰
為一腰作等腰![]() ,使
,使![]() ,且
,且![]() ,設(shè)
,設(shè)![]() ,
,![]() ,我們稱
,我們稱![]() 為
為![]() 的“頂補(bǔ)三角形”.
的“頂補(bǔ)三角形”.
(1)求![]() 與
與![]() 的數(shù)量關(guān)系;
的數(shù)量關(guān)系;
(2)如圖2,![]() 為
為![]() 的“頂補(bǔ)三角形”,過點(diǎn)
的“頂補(bǔ)三角形”,過點(diǎn)![]() 作
作![]() 的平行線,交
的平行線,交![]() 于點(diǎn)
于點(diǎn)![]() ,若四邊形
,若四邊形![]() 是平行四邊形,求證:
是平行四邊形,求證:![]() ;
;
(3)如圖3,四邊形![]() 中,
中,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 在
在![]() 上,
上,![]() ,
,![]() B,
B,![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ;(2)見解析;(3)
;(2)見解析;(3)![]()
【解析】
(1)根據(jù)等腰三角形的內(nèi)角關(guān)系可以得到![]() ,
,![]() ,再結(jié)合
,再結(jié)合![]() ,即可求出
,即可求出![]() 和
和![]() 的關(guān)系;
的關(guān)系;
(2)由于四邊形![]() 是平行四邊形,所以
是平行四邊形,所以![]() ,則
,則![]() ,同時由
,同時由![]() 得到
得到![]() ,在(1)中得到“頂補(bǔ)三角形”的性質(zhì),
,在(1)中得到“頂補(bǔ)三角形”的性質(zhì),![]() ,所以
,所以![]() ,即可得證;
,即可得證;
(3)連接![]() ,由已知條件可以證得
,由已知條件可以證得![]() ,所以
,所以![]() ,根據(jù)三角形的外角定理可以得到
,根據(jù)三角形的外角定理可以得到![]() ,結(jié)合已知條件
,結(jié)合已知條件![]() ,可以得到
,可以得到![]() ,而
,而![]() ,
,![]() ,所以
,所以![]() 是
是![]() 的“頂補(bǔ)三角形”,結(jié)合在(1)中得到“頂補(bǔ)三角形”的性質(zhì)可以得到
的“頂補(bǔ)三角形”,結(jié)合在(1)中得到“頂補(bǔ)三角形”的性質(zhì)可以得到![]() ,過點(diǎn)
,過點(diǎn)![]() 分別作
分別作![]() ,
,![]() 上的高
上的高![]() ,
,![]() ,可以證得
,可以證得![]() ,相似比為
,相似比為![]() ,所以
,所以![]() ,與此同時結(jié)合等腰三角形的性質(zhì)可以得
,與此同時結(jié)合等腰三角形的性質(zhì)可以得![]() ,
,![]() ,所以
,所以![]() ,而
,而![]() ,所以
,所以![]() ,
,
則![]() ,即可求解;
,即可求解;
解:(1)∵在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
![]() .
.
![]() .
.
(2)![]() 為
為![]() 的“頂補(bǔ)三角形”,
的“頂補(bǔ)三角形”,
![]() ,
,![]() .
.
![]() 四邊形
四邊形![]() 是平行四邊形,
是平行四邊形,
![]()
![]() .
.
![]() .
.
![]() .
.
![]() .
.
(3)連接![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() .
.![]() .
.
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
又![]() ,
,![]() ,
,
![]() 是
是![]() 的“頂補(bǔ)三角形”.
的“頂補(bǔ)三角形”.
![]() .
.
過點(diǎn)![]() 分別作
分別作![]() ,
,![]() 上的高
上的高![]() ,
,![]() .
.
則有![]() .
.
![]() .
.
同理可證![]() .
.
![]() .
.
![]() ,
,![]() 分別是等腰
分別是等腰![]() 與等腰
與等腰![]() 底邊上的高,
底邊上的高,
![]() ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() .
.
![]() .
.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
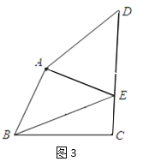
【題目】已知∠ACD=90°,AC=DC,MN是過點(diǎn)A的直線,DB⊥MN于點(diǎn)B.
(1)如圖,求證:BD+AB=![]() BC;
BC;
(2)直線MN繞點(diǎn)A旋轉(zhuǎn),在旋轉(zhuǎn)過程中,當(dāng)∠BCD=30°,BD=![]() 時,求BC的值.
時,求BC的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知二次函數(shù)![]() (
(![]() 為常數(shù),
為常數(shù),![]() )的圖象過點(diǎn)
)的圖象過點(diǎn)![]() 和點(diǎn)
和點(diǎn)![]() ,函數(shù)圖象最低點(diǎn)
,函數(shù)圖象最低點(diǎn)![]() 的縱坐標(biāo)為
的縱坐標(biāo)為![]() .直線
.直線![]() 的解析式為
的解析式為![]()
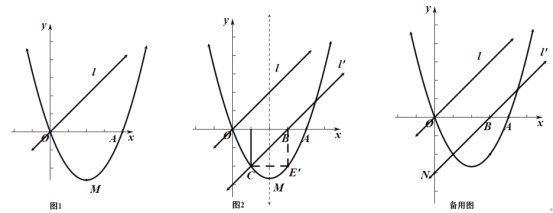
![]() 求二次函數(shù)的解析式;
求二次函數(shù)的解析式;
![]() 直線
直線![]() 沿
沿![]() 軸向右平移,得直線
軸向右平移,得直線![]() ,
,![]() 與線段
與線段![]() 相交于點(diǎn)
相交于點(diǎn)![]() ,與
,與![]() 軸下方的拋物線相交于點(diǎn)
軸下方的拋物線相交于點(diǎn)![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,把
,把![]() 沿直線
沿直線![]() 折疊,當(dāng)點(diǎn)
折疊,當(dāng)點(diǎn)![]() 恰好落在拋物線上點(diǎn)
恰好落在拋物線上點(diǎn)![]() 時(圖
時(圖![]() 求直線
求直線![]() 的解析式;
的解析式;
![]() 在
在![]() 的條件下,
的條件下,![]() 與
與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,把
,把![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() 得到
得到![]() ,P為
,P為![]() 上的動點(diǎn),當(dāng)
上的動點(diǎn),當(dāng)![]() 為等腰三角形時,求符合條件的點(diǎn)
為等腰三角形時,求符合條件的點(diǎn)![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
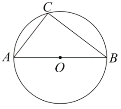
【題目】如圖,![]() 是
是![]() 的直徑,點(diǎn)
的直徑,點(diǎn)![]() 在
在![]() 上,點(diǎn)
上,點(diǎn)![]() 是
是![]() 上一動點(diǎn),且與點(diǎn)
上一動點(diǎn),且與點(diǎn)![]() 分別位于直徑
分別位于直徑![]() 的兩側(cè),
的兩側(cè),![]() ,過點(diǎn)
,過點(diǎn)![]() 作
作![]() 交
交![]() 的延長線于點(diǎn)
的延長線于點(diǎn)![]() ;
;

(1)當(dāng)點(diǎn)![]() 運(yùn)動到什么位置時,
運(yùn)動到什么位置時,![]() 恰好是
恰好是![]() 的切線?畫出圖形并加以說明.
的切線?畫出圖形并加以說明.
(2)若點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 關(guān)于直徑
關(guān)于直徑![]() 對稱,且
對稱,且![]() ,畫出圖形求此時
,畫出圖形求此時![]() 的長.
的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】將如圖所示的牌面數(shù)字分別是1,2,3,4的四張撲克牌背面朝上,洗勻后放在桌面上.
(1)從中隨機(jī)抽出一張牌,牌面數(shù)字是偶數(shù)的概率是__________;
(2)先從中隨機(jī)抽出一張牌,將牌面數(shù)字作為十位上的數(shù)字(不放回),再隨機(jī)抽取一張,將牌面數(shù)字作為個位上的數(shù)字,請用畫樹狀圖或列表的方法求組成的兩位數(shù)恰好是3的倍數(shù)的概率.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】綜合與實(shí)踐
問題情境
在綜合與實(shí)踐課上,同學(xué)們以“三角形的折疊”為主題開展數(shù)學(xué)活動.
操作發(fā)現(xiàn)
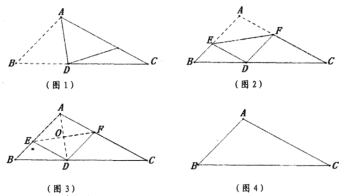
“楊輝”小組的同學(xué)用一張鈍角三角形紙片![]() ,
,![]() 為鈍角,進(jìn)行了如下操作:
為鈍角,進(jìn)行了如下操作:
第一步:如圖1,折出![]() 的角平分線
的角平分線![]() ;
;
第二步:如圖2,展平紙片,再次折疊該三角形紙片,使預(yù)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合,拆痕
重合,拆痕![]() 分別與
分別與![]() ,
,![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() ;
;
第三步:如圖3,再次展平紙片,連接![]() ,
,![]() ,可得四邊形
,可得四邊形![]() .
.
(1)在圖4的![]() 中利用尺規(guī)作出折痕
中利用尺規(guī)作出折痕![]() ,
,![]() ;
;
(要求:保留作圖痕跡,不寫作法)
實(shí)踐探究
(2)試判斷圖3中四邊形![]() 的形狀,并寫出證明過程;
的形狀,并寫出證明過程;
深入探究
(3)“陳景潤”小組的同學(xué)突發(fā)奇想,在“楊輝”小組同學(xué)操作的基礎(chǔ)上設(shè)計(jì)了這樣一個問題:在圖3中,連接![]() ,分別交
,分別交![]() 于點(diǎn)
于點(diǎn)![]() ,交
,交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,
,![]() ,利用相似三角形的知識可以求出
,利用相似三角形的知識可以求出![]() 的長.請你寫出求解過程.
的長.請你寫出求解過程.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,以Rt△ABC的斜邊BC為一邊在△ABC的同側(cè)作正方形BCEF,設(shè)正方形的中心為O,連接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
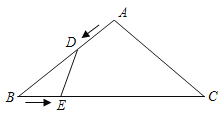
【題目】如圖所示,在等腰△ABC中,AB=AC=10cm,BC=16cm.點(diǎn)D由點(diǎn)A出發(fā)沿AB方向向點(diǎn)B勻速運(yùn)動,同時點(diǎn)E由點(diǎn)B出發(fā)沿BC方向向點(diǎn)C勻速運(yùn)動,它們的速度均為1cm/s.連接DE,設(shè)運(yùn)動時間為t(s)(0<t<10),解答下列問題:
(1)當(dāng)t為何值時,△BDE的面積為7.5cm2;
(2)在點(diǎn)D,E的運(yùn)動中,是否存在時間t,使得△BDE與△ABC相似?若存在,請求出對應(yīng)的時間t;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖所示,矩形ABCD中,AB=5,BC=8,點(diǎn)P為BC上一動點(diǎn)(不與端點(diǎn)重合),連接AP,將△ABP沿著AP折疊.點(diǎn)B落到M處,連接BM、CM,若△BMC為等腰三角形,則BP的長度為_____.

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com