
【題目】如圖1,已知拋物線y=﹣![]() x2+
x2+![]() x+
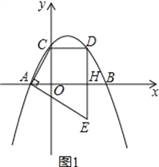
x+![]() 與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,點D是點C關于拋物線對稱軸的對稱點,連接CD,過點D作DH⊥x軸于點H,過點A作AE⊥AC交DH的延長線于點E.
與x軸交于A,B兩點(點A在點B的左側),與y軸交于點C,點D是點C關于拋物線對稱軸的對稱點,連接CD,過點D作DH⊥x軸于點H,過點A作AE⊥AC交DH的延長線于點E.
(1)求線段DE的長度;
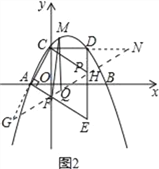
(2)如圖2,試在線段AE上找一點F,在線段DE上找一點P,且點M為直線PF上方拋物線上的一點,求當△CPF的周長最小時,△MPF面積的最大值是多少;
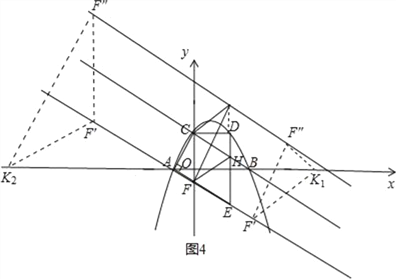
(3)在(2)問的條件下,將得到的△CFP沿直線AE平移得到△C′F′P′,將△C′F′P′沿C′P′翻折得到△C′P′F″,記在平移過稱中,直線F′P′與x軸交于點K,則是否存在這樣的點K,使得△F′F″K為等腰三角形?若存在求出OK的值;若不存在,說明理由.

【答案】(1)2![]() ;(2)
;(2) ![]() ;(3)見解析.
;(3)見解析.
【解析】分析:(1)根據解析式求得C的坐標,進而求得D的坐標,即可求得DH的長度,令y=0,求得A,B的坐標,然后證得△ACO∽△EAH,根據對應邊成比例求得EH的長,進繼而求得DE的長;
(2)找點C關于DE的對稱點N(4,![]() ),找點C關于AE的對稱點G(-2,-
),找點C關于AE的對稱點G(-2,-![]() ),連接GN,交AE于點F,交DE于點P,即G、F、P、N四點共線時,△CPF周長=CF+PF+CP=GF+PF+PN最小,根據點的坐標求得直線GN的解析式:y=
),連接GN,交AE于點F,交DE于點P,即G、F、P、N四點共線時,△CPF周長=CF+PF+CP=GF+PF+PN最小,根據點的坐標求得直線GN的解析式:y=![]() x-
x-![]() ;直線AE的解析式:y= -
;直線AE的解析式:y= -![]() x-
x-![]() ,過點M作y軸的平行線交FH于點Q,設點M(m,-
,過點M作y軸的平行線交FH于點Q,設點M(m,-![]() m+
m+![]() m+
m+![]() ),則Q(m,
),則Q(m,![]() m-
m-![]() ),根據S△MFP=S△MQF+S△MQP,得出S△MFP= -
),根據S△MFP=S△MQF+S△MQP,得出S△MFP= -![]() m+
m+![]() m+
m+![]() ,根據解析式即可求得,△MPF面積的最大值;
,根據解析式即可求得,△MPF面積的最大值;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),求得CF=
),求得CF=![]() ,CP=
,CP=![]() ,進而得出△CFP為等邊三角形,邊長為
,進而得出△CFP為等邊三角形,邊長為![]() ,翻折之后形成邊長為
,翻折之后形成邊長為![]() 的菱形C′F′P′F″,且F′F″=4,然后分三種情況討論求得即可.
的菱形C′F′P′F″,且F′F″=4,然后分三種情況討論求得即可.
本題解析:(1)對于拋物線y=﹣![]() x2+
x2+![]() x+
x+![]() ,
,
令x=0,得y=![]() ,即C(0,
,即C(0,![]() ),D(2,
),D(2,![]() ),
),
∴DH=![]() ,
,
令y=0,即﹣![]() x2+
x2+![]() x+
x+![]() =0,得x1=﹣1,x2=3,
=0,得x1=﹣1,x2=3,
∴A(﹣1,0),B(3,0),
∵AE⊥AC,EH⊥AH,
∴△ACO∽△EAH,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:EH=![]() ,
,
則DE=2![]() ;
;
(2)找點C關于DE的對稱點N(4,![]() ),找點C關于AE的對稱點G(﹣2,﹣
),找點C關于AE的對稱點G(﹣2,﹣![]() ),
),
連接GN,交AE于點F,交DE于點P,即G、F、P、N四點共線時,△CPF周長=CF+PF+CP=GF+PF+PN最小,
直線GN的解析式:y=![]() x﹣
x﹣![]() ;直線AE的解析式:y=﹣
;直線AE的解析式:y=﹣![]() x﹣
x﹣![]() ,
,
聯立得:F (0,﹣![]() ),P(2,
),P(2,![]() ),
),
過點M作y軸的平行線交FH于點Q,
設點M(m,﹣![]() m2+
m2+![]() m+
m+![]() ),則Q(m,
),則Q(m,![]() m﹣
m﹣![]() ),(0<m<2);
),(0<m<2);
∴S△MFP=S△MQF+S△MQP=![]() MQ×2=MQ=﹣
MQ×2=MQ=﹣![]() m2+
m2+![]() m+
m+![]()
![]() ,
,
∵對稱軸為:直線m=![]() <2,開口向下,
<2,開口向下,
∴m=![]() 時,△MPF面積有最大值:
時,△MPF面積有最大值:![]()
![]() ;
;
(3)由(2)可知C(0,![]() ),F(0,
),F(0,![]() ),P(2,
),P(2,![]() ),
),
∴CF=![]() ,CP=
,CP=![]() =
=![]() ,
,
∵OC=![]() ,OA=1,
,OA=1,
∴∠OCA=30°,
∵FC=FG,
∴∠OCA=∠FGA=30°,
∴∠CFP=60°,
∴△CFP為等邊三角形,邊長為![]() ,
,
翻折之后形成邊長為![]() 的菱形C′F′P′F″,且F′F″=4,
的菱形C′F′P′F″,且F′F″=4,
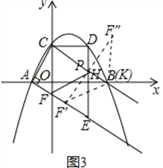
1)當K F′=KF″時,如圖3,
點K在F′F″的垂直平分線上,所以K與B重合,坐標為(3,0),
∴OK=3;
2)當F′F″=F′K時,如圖4,
∴F′F″=F′K=4,
∵FP的解析式為:y=x﹣
![]() ,
,
∴在平移過程中,F′K與x軸的夾角為30°,
∵∠OAF=30°,
∴F′K=F′A
∴AK=4![]()
∴OK=4![]() ﹣1或者4
﹣1或者4![]() +1;
+1;
3)當F″F′=F″K時,如圖5,
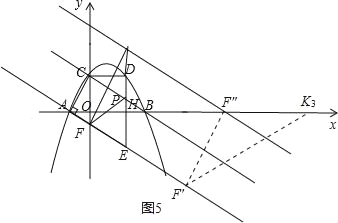
∵在平移過程中,F″F′始終與x軸夾角為60°,
∵∠OAF=30°,
∴∠AF′F″=90°,
∵F″F′=F″K=4,
∴AF″=8,
∴AK=12,
∴OK=11,
綜上所述:OK=3,4![]() ﹣1,4
﹣1,4![]() +1或者11.
+1或者11.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:
【題目】已知:如圖,一次函數![]() 與
與![]() 的圖象相交于點
的圖象相交于點![]() .
.

(1)求點![]() 的坐標.
的坐標.
(2)若一次函數![]() 與
與![]() 的圖象與
的圖象與![]() 軸分別相交于點
軸分別相交于點![]() 、
、![]() ,求
,求![]() 的面積.
的面積.
(3)結合圖象,直接寫出![]() 時
時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩車分別從A,B兩地同時相向勻速行駛,當乙車到達A地后,繼續保持原速向遠離B的方向行駛,而甲車到達B地后立即掉頭,并保持原速與乙車同向行駛,經過15小時后兩車同時到達距A地300千米的C地(中途休息時間忽略不計).設兩車行駛的時間為x(小時),兩車之間的距離為y(千米),y與x之間的函數關系如圖所示,則當甲車到達B地時,乙車距A地_____千米.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CA⊥AB,垂足為點A,AB=10,AC=5,射線BM⊥AB,垂足為點B,一動點E從A點出發以2厘米秒的速度沿射線AN包括點A)運動,點D為射線BM上一動點,隨著E點運動而運動,且始終保持ED=CB,當點E運動_____秒時,△DEB與△BCA全等.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,放在直角坐標系中的正方形ABCD邊長為4,現做如下實驗:拋擲一枚均勻的正四面體骰子(它有四個頂點,各頂點的點數分別是1至4這四個數字中一個),每個頂點朝上的機會是相同的,連續拋擲兩次,將骰子朝上的頂點數作為直角坐標中P點的坐標)第一次的點數作橫坐標,第二次的點數作縱坐標).
(1)求P點落在正方形ABCD面上(含正方形內部和邊界)的概率.
(2)將正方形ABCD平移整數個單位,則是否存在一種平移,使點P落在正方形ABCD
面上的概率為0.75;若存在,指出其中的一種平移方式;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=90°,∠A=30°,AC=2.將△ABC繞點C順時針旋轉120°得△A′B′C.
(1)求作:△A′B′C;
(2)求點B旋轉經過的路徑長;
(3)求線段BB′的長;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠BAC=90°,AC=2AB,點D是AC的中點.將一塊銳角為45°的直角三角板如圖放置,使三角板斜邊的兩個端點分別與A、D重合,連接BE、EC.
 試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
試猜想線段BE和EC的數量及位置關系,并證明你的猜想.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com