
【題目】問題情境:
在綜合實踐課上,張老師讓同學們以“矩形的折疊”為主題開展數學活動,張老師拿著一張矩形紙片ABCD,其中AB=acm, AD=bcm, 如圖1,先沿對角線BD折疊,點C落在點E的位置,BE交AD于點F.
操作發現:
(1)“奮進”小組發現與BF的長度一定相等的線段是哪一條;
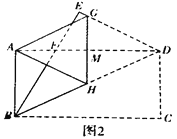
(2)如圖2.“雄鷹”小組將圖1再折疊一次,使點D與點A重合,得到折痕GH,GH交AD于點M,發現△DGH是等腰三角形,請你證明這個結論;
實踐探究:
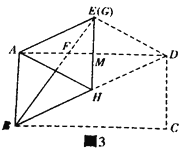
(3)“創新”小組將自己準備的矩形紙片按照(2)中“雄鷹”小組的作法操作,發現點E和點G重合,,如圖3,試探究“創新”小組準備的矩形紙片中a與b滿足的數量關系;
(4)”愛心”小組在其他小組的基礎上提出問題:當a與b滿足什么關系時,點G是DE的中點?請你直接出a與b滿足的關系.
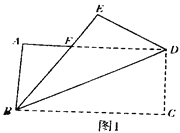
【答案】(1)BF=DF,(2)△DGH是等腰三角形,(3)b=![]() (4)a=b
(4)a=b
【解析】
(1)根據折疊的條件,證明△AFB≌△EFD(AAS)即可解題,
(2)找到對稱軸,證明GH平行CD,利用內錯角相等得∠GHD=∠HDC,由折疊得∠GDH=∠GHD,等量代換得∠GDH=∠GHD,等角對等邊即可解題.
(3)在Rt△BED中利用斜邊中線等于斜邊一半,得BD=2EH,根據已知,用代數式表示出BD和EH的長即可解題,
(4)根據題意,證明四邊形ABCD是正方形,即可直接寫出a=b的結論.
解:(1)BF=DF,
由折疊可知:AB=DE,∠A=∠E,∠AFB=∠EFD,
∴△AFB≌△EFD(AAS)
∴BF=DF,
(2)由(1)可知∠GDH=∠HDC
由圖可知:GH為對稱軸,點D和點A關于GH對稱,即GH垂直平分AD,
∵四邊形ABCD是矩形,AD⊥CD,
∴GH∥CD,
∴∠GHD=∠HDC
∴∠GDH=∠GHD
∴△DGH是等腰三角形,
(3)由題可知,點H為對角線BD上的中點,EH=ED,
在Rt△BED中,BD=2EH(斜邊中線等于斜邊一半)
∵AB=acm, AD=bcm,
∴EH=ED=AB= a,BD=![]()
∴![]() =a,整理得:b=
=a,整理得:b=![]()
(4)a=b
理由:根據題意可知,GH為中位線,GH∥EB,點A與E重合,此時圖形為正方形,
故a=b


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
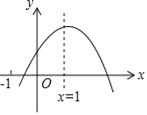
【題目】已知二次函數y=ax2+bx+c的圖象如圖所示,給出下列結論:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若點(﹣![]() ,y1)和(
,y1)和(![]() ,y2)在該圖象上,則y1>y2.其中正確的結論是_____(填入正確結論的序號)
,y2)在該圖象上,則y1>y2.其中正確的結論是_____(填入正確結論的序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】四位同學在研究函數y=x2+bx+c(b,c是常數)時,甲發現當x=1時,函數有最小值;乙發現﹣1是方程x2+bx+c=0的一個根;丙發現函數的最小值為3;丁發現當x=2時,y=4,已知這四位同學中只有一位發現的結論是錯誤的,則該同學是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ACBE內接于⊙O,AB平分∠CAE,CD⊥AB交AB、AE分別于點H、D.

(1)如圖①,求證:BD=BE;
(2)如圖②,若F是弧AC的中點,連接BF,交CD于點M,∠CMF=2∠CBF,連接FO、OC,求∠FOC的度數;
(3)在(2)的條件下,連接OD,若BC=4![]() ,OD=7,求BF的長.
,OD=7,求BF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)現有5個質地、大小完全相同的小球上分別標有數字﹣1,﹣2,1,2,3.先將標有數字﹣2,1,3的小球放在第一個不透明的盒子里,再將其余小球放在第二個不透明的盒子里.現分別從兩個盒子里各隨即取出一個小球.
(1)請利用列表或畫樹狀圖的方法表示取出的兩個小球上數字之和所有可能的結果;
(2)求取出的兩個小球上的數字之和等于0的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是半徑為4的⊙O的直徑,P是圓上異于A,B的任意一點,∠APB的平分線交⊙O于點 C,連接AC和BC,△ABC的中位線所在的直線與⊙O相交于點E、F,則EF的長是________

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a滿足以下三個條件:①a是整數;②關于x的一元二次方程ax2+4x﹣2=0有兩個不相等的實數根;③反比例函數![]() 的圖象在第二、四象限.
的圖象在第二、四象限.
(1)求a的值.
(2)求一元二次方程ax2+4x﹣2=0的根.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系xoy中,點M在x軸的正半軸上,⊙M交x軸于A、B兩點,交y軸于C、D兩點,且C為弧AE的中點,AE交y軸于G點,若點A的坐標為(-1,0),AE=4
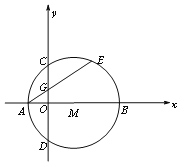
(1)求點C的坐標;
(2)連接MG、BC,求證:MG∥BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,禁漁期間,我漁政船在A處發現正北方向B處有一艘可疑船只,測得A、B兩處距離為99海里,可疑船只正沿南偏東53°方向航行.我漁政船迅速沿北偏東27°方向前去攔截,2小時后剛好在C處將可疑船只攔截.求該可疑船只航行的速度.
(參考數據:sin27°≈![]() , cos27°≈
, cos27°≈![]() , tan27°≈
, tan27°≈![]() , sin53°≈
, sin53°≈![]() , cos53°≈
, cos53°≈![]() , tan53°≈
, tan53°≈![]() )
)
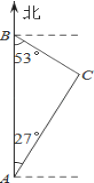
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com