不定方程a2+b2+c2=a2b2的所有整數解是 .
【答案】
分析:首先對其中c進行分析,c等于零 奇數 偶數再對a b分析(同為奇數 偶數 一奇一偶),求出每種情況的解的情況,再依次進行分析,最終求出方程的解.只有一個解.
解答:解:首先對c進行奇偶性分析:
(1)c=0時,方程化為a
2+b
2=a
2b
2,即(a
2-1)(b
2-1)=1由于a
2-1與b
2-1都是1的約數,
所以
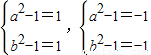
以上方程組只能解出a=b=0,于是,方程有一組解a=b=c=0.
(2)c為奇數時,再對a,b進行奇偶性分析.
(i)若a和b同為奇數,則a
2,b
2,c
2都是4k+1型,于是a
2+b
2+c
2為4k+3型,而a
2b
2為4k+1型,等式不能成立,方程無解;
(ii)若a,b同為偶數,此時方程左邊=a
2+b
2+c
2為奇數,左邊=a
2b
2為偶數,方程無解;
(iii)若a和b為一奇一偶,此時方程左邊為4k+2型,右邊為4k時,方程無解.
(3)c為偶數時,仍對a和b進行奇偶性分析:
(i)若a和b同為奇數,則方程左邊為4k+2型,右邊為奇數,方程無解;
(ii)若a和b為一奇一偶,則方程左邊為奇數,右邊為偶數,方程無解;
(iii)若a,b同為偶數,這時,方程兩邊均為4k型,需要再細致分析:
設a=2
mα,b=2
nβ,c=2
tr,其中m,n,t為非負整數,α,β,r為奇數.則方程化為2
2mα
2+2
2nβ
2+2
2tr
2=2
2m+2nα
2β
2當t最小時,方程兩邊約去2
2t,得2
2m-2tα
2+2
2n-2tβ
2+r
2=α
2β
2•2
2m+2n-2t顯然,方程左邊為奇數,右邊為偶數,方程無解;
當m最小時,方程兩邊約去2
2m得α
2+2
2n-2mβ
2+2
2t-2mr
2=2
2nα
2β
2.
同樣,方程左邊為奇數,右邊為偶數,方程無解;
當n最小時,同樣可得方程無解.
當m=n=t時,則方程左邊是奇數,而右邊是偶數,方程無解;
綜上討論,方程a
2+b
2+c
2=a
2b
2只有一組整數解a=0,b=0,c=0.
點評:解此題的關鍵是如何對abc進行分析,分析要全面(如奇數偶數零),求出所有情況的方程的解,再針對所有的進行歸納和總結.

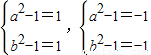 以上方程組只能解出a=b=0,于是,方程有一組解a=b=c=0.
以上方程組只能解出a=b=0,于是,方程有一組解a=b=c=0.
