
【題目】四邊形ABCD中,∠BAD的角平分線與邊BC交于點E,∠ADC的角平分線交直線AE于點O.
(1)若點O在四邊形ABCD的內部,
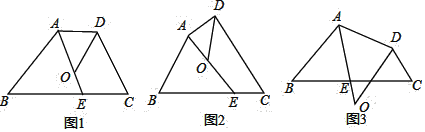
①如圖1,若AD∥BC,∠B=40°,∠C=70°,則∠DOE= °;
②如圖2,試探索∠B、∠C、∠DOE之間的數(shù)量關系,并將你的探索過程寫下來.
(2)如圖3,若點O在四邊形ABCD的外部,請你直接寫出∠B、∠C、∠DOE之間的數(shù)量關系.
【答案】(1)①125;②∠B+∠C+2∠DOE=360°,理由詳見解析;(2)∠B+∠C=2∠DOE,理由詳見解析.
【解析】
(1)①根據(jù)平行線的性質和角平分線的定義可求∠BAE,∠CDO,再根據(jù)三角形外角的性質可求∠AEC,再根據(jù)四邊形內角和等于360°可求∠DOE的度數(shù);
②根據(jù)三角形外角的性質和角平分線的定義可得∠DOE和∠BAD、∠ADC的關系,再根據(jù)四邊形內角和等于360°可求∠B、∠C、∠DOE之間的數(shù)量關系;
(2)根據(jù)四邊形和三角形的內角和得到∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,根據(jù)角平分線的定義得到∠BAD=2∠EAD,∠ADC=2∠ADO,于是得到結論.
解:(1)①∵AD∥BC,∠B=40°,∠C=70°,
∴∠BAD=140°,∠ADC=110°,
∵AE、DO分別平分∠BAD、∠CDA,
∴∠BAE=70°,∠ODC=55°,
∴∠AEC=110°,
∴∠DOE=360°-110°-70°-55°=125°;
故答案為:125;
②∠B+∠C+2∠DOE=360°,
理由:∵∠DOE=∠OAD+∠ADO,
∵AE、DO分別平分∠BAD、∠CDA,
∴2∠DOE=∠BAD+∠ADC,
∵∠B+∠C+∠BAD+∠ADC=360°,
∴∠B+∠C+2∠DOE=360°;
(2)∠B+∠C=2∠DOE,
理由:∵∠BAD+∠ADC=360°-∠B-∠C,∠EAD+∠ADO=180°-∠DOE,
∵AE、DO分別平分∠BAD、∠CDA,
∴∠BAD=2∠EAD,∠ADC=2∠ADO,
∴∠BAD+∠ADC=2(∠EAD+∠ADO),
∴360°-∠B-∠C=2(180°-∠DOE),
∴∠B+∠C=2∠DOE.


科目:初中數(shù)學 來源: 題型:
【題目】觀察下列式子,并解決問題.
![]() ≈0.1260;
≈0.1260;![]() ≈0.2714;
≈0.2714;![]() ≈0.5848;
≈0.5848;![]() ≈1.260;
≈1.260;![]() ≈2.714.
≈2.714.
(1)![]() ≈ ,
≈ ,![]() ≈ ;
≈ ;
(2)若![]() ≈58.48,則x≈ ;
≈58.48,則x≈ ;
(3)通過類比,你能得到什么規(guī)律?用一句話描述出來.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系中,三角形ABC的三個頂點的位置如圖所示,點A'的坐標是(-2,2),現(xiàn)將三角形ABC平移,使點A變換為點A',點B',C'分別是B,C的對應點.
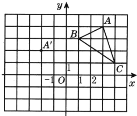
(1)請畫出平移后的三角形A'B'C'(不寫畫法),并直接寫出B',C'的坐標;
(2)若三角形ABC內部一點P的坐標為(a,b),則點P的對應點P'的坐標是_______.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:如圖,在矩形ABCD中,AB=6cm,BC=8cm,對角線AC,BD交于點O,點P從點A出發(fā),沿AD方向勻速運動,速度為1cm/s;同時,點Q從點D出發(fā),沿DC方向勻速運動,速度為1cm/s;當一個點停止運動時,另一個點也停止運動.連接PO并延長,交BC于點E,過點Q作QF∥AC,交BD于點F.設運動時間為t(s)(0<t<6),解答下列問題: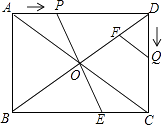
(1)當t為何值時,AP=PO.
(2)設五邊形OECQF的面積為S(cm2),試確定S與t的函數(shù)關系式;
(3)在運動過程中,是否存在某一時刻t,使OD平分∠COP?若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如圖所示放置,點A1 , A2 , A3 , 和點C1 , C2 , C3 , …,分別在直線y=kx+b(k>0)和x軸上,已知點B1 , B2 , B3 , B4的坐標分別為(1,1)(3,2),(7,4),(15,8),則Bn的坐標是( ) 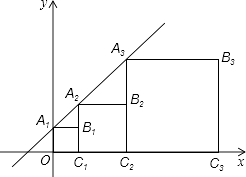
A.(2n﹣1,2n﹣1)
B.(2n , 2n﹣1)
C.(2n﹣1 , 2n)
D.(2n﹣1﹣1,2n﹣1)
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
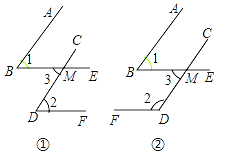
【題目】已知一個角的兩邊與另一個角的兩邊分別平行,請結合圖,探索這兩個角之間的關系,并說明理由.
(1)如圖①,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(2)如圖②,AB∥CD,BE∥DF,∠1與∠2的關系是 ;
證明:
(3)經(jīng)過上述證明,我們可得出結論,如果一個角的兩邊與另一個角的兩邊分別平行,那么這兩個角 ;
(4)若這兩個角的兩邊分別平行,且一個角比另一個角的3倍少60°,則這兩個角分別是多少度?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在邊長為1的小正方形網(wǎng)格中,△AOB的頂點均在格點上.
(1)B點關于y軸的對稱點坐標為 ;
(2)將△AOB向左平移3個單位長度得到△A1O1B1,請畫出△A1O1B1;
(3)在(2)的條件下,A1的坐標為 .

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
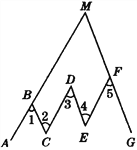
【題目】如圖,在折線ABCDEFG中,已知∠1=∠2=∠3=∠4=∠5,延長AB、GF交于點M.試探索∠AMG與∠3的關系,并說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
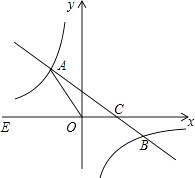
【題目】如圖,在平面直角坐標系xOy中,一次函數(shù)y=kx+b(k≠0)的圖象與反比例函數(shù) ![]() 的圖象交于二四象限內的A、B 兩點,與x軸交于C點,點B的坐標為(6,n),線段OA=5,E為x軸負半軸上一點,且sin∠AOE=
的圖象交于二四象限內的A、B 兩點,與x軸交于C點,點B的坐標為(6,n),線段OA=5,E為x軸負半軸上一點,且sin∠AOE= ![]() .
. 
(1)求該反比例函數(shù)和一次函數(shù)的解析式;
(2)求△AOC的面積;
(3)直接寫出一次函數(shù)值大于反比例函數(shù)值時自變量x的取值范圍.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com