
【題目】對于拋物線![]() ,下列說法錯誤的是( )
,下列說法錯誤的是( )
A.若頂點在x軸下方,則一元二次方程![]() 有兩個不相等的實數根
有兩個不相等的實數根
B.若拋物線經過原點,則一元二次方程![]() 必有一根為0
必有一根為0
C.若![]() ,則拋物線的對稱軸必在y軸的左側
,則拋物線的對稱軸必在y軸的左側
D.若![]() ,則一元二次方程
,則一元二次方程![]() ,必有一根為-2
,必有一根為-2
【答案】A
【解析】
A:當頂點在x軸的下方且開口向下時,此時可根據拋物線與橫軸的交點個數來判斷一元二次方程的解的情況;
B:當拋物線經過原點時,此時c=0,可求出一元二次方程ax2+bx+c=0的一根;
C:a與b的符合共同決定了拋物線的對稱軸的位置;
D:可將方程的根代入一元二次方程求得a、b、c之間的關系.
解:A:當頂點在x軸的下方且a<0時,
此時拋物線與x軸沒有交點,
∴一元二次方程ax2+bx+c=0沒有實數根,
∴A錯誤;
B:當拋物線經過原點時,c=0,
∴ax2+bx=0,
解得:x=0或x=-![]() ,
,
∴一元二次方程ax2+bx+c=0必有一根為0,
∴B正確;
C:∵拋物線的對稱軸為:x=-![]() ,
,
∴拋物線的對稱軸的位置由與b的符合共同決定,
∴C正確;
D:令x=-2,得:4a-2b+c=0,
∴2b=4a+c,
∴D正確,
故選A.


科目:初中數學 來源: 題型:
【題目】某校組織學生書法比賽,對參賽作品按A、B、C、D四個等級進行了評定.現隨機取部分學生書法作品的評定結果進行分析,并繪制扇形統計圖和條形統計圖如下:

根據上述信息完成下列問題:
(1)求這次抽取的樣本的容量;
(2)請在圖②中把條形統計圖補充完整;
(3)已知該校這次活動共收到參賽作品750份,請你估計參賽作品達到B級以上(即A級和B級)有多少份?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某校九年級學生體育測試成績情況,現從中隨機抽取部分學生的體育成績,并用得到的數據繪制了統計圖①和圖②,請根據圖中提供的信息,回答下列問題:
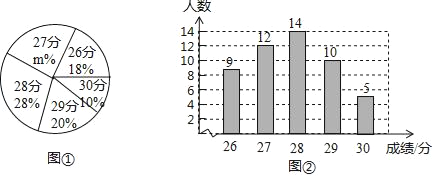
(1)本次隨機抽樣調查的學生人數為______,圖①中的m的值為______;
(2)求本次抽樣調查獲取的樣本數據的眾數、中位數和平均數;
(3)若該校九年級共有學生300人,如果體育成績達28分以上(含28分)為優秀,請估計該校九年級學生體育成績達到優秀的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有![]() ,
,![]() 兩個不透明的袋子,分別裝有3個除顏色外完全相同的小球.其中,
兩個不透明的袋子,分別裝有3個除顏色外完全相同的小球.其中,![]() 袋裝有1個白球,2個紅球;
袋裝有1個白球,2個紅球;![]() 袋裝有1個紅球,2個白球.
袋裝有1個紅球,2個白球.
(1)將![]() 袋搖勻,然后從
袋搖勻,然后從![]() 袋中隨機摸出一個球,則摸出的小球是紅球的概率為______;
袋中隨機摸出一個球,則摸出的小球是紅球的概率為______;
(2)小王和小周商定了一個游戲規則:從搖勻后的![]() ,
,![]() 兩袋中各隨機摸出一個球,摸出的這兩個球,若顏色相同,則小王獲勝;若顏色不同,則小周獲勝.請利用概率說明這個游戲規則是否公平.
兩袋中各隨機摸出一個球,摸出的這兩個球,若顏色相同,則小王獲勝;若顏色不同,則小周獲勝.請利用概率說明這個游戲規則是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新冠病毒潛伏期較長,能通過多種渠道傳播,以在生活中就要做好最基本的防護:在公共區域和陌生人保持距離,勤洗手,出門戴口罩某區中小學陸續復學后,為了提高同學們的防疫意識,決定組織防疫知識競賽活動,評出一、二三等獎各若干名,并分別發給洗手液、溫度計和口罩作為獎品.
(1)如果溫度計的單價比口罩的單價多![]() 元,購買洗手液
元,購買洗手液![]() 瓶和口罩
瓶和口罩![]() 個共需
個共需![]() 元;購買
元;購買![]() 瓶洗手液比購買
瓶洗手液比購買![]() 支溫度計多花
支溫度計多花![]() 元,求洗手液、溫度計和口罩的單價各是多少元?
元,求洗手液、溫度計和口罩的單價各是多少元?
(2)已知本次競賽活動獲得三等獎的人數是獲得二等獎人數的![]() 倍,且獲得一等獎的人數不超過獲獎總人數的五分之一,如果購買這三種獎品的總費用為
倍,且獲得一等獎的人數不超過獲獎總人數的五分之一,如果購買這三種獎品的總費用為![]() 元,求本次競賽活動獲得一、二、三等獎各有多少人.
元,求本次競賽活動獲得一、二、三等獎各有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
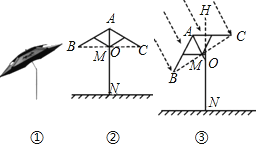
【題目】如圖①是釣魚傘,為遮擋不同方向的陽光,釣魚傘可以在撐桿AN上的點O處彎折并旋轉任意角,圖②是釣魚傘直立時的示意圖,當傘完全撐開時,傘骨AB,AC與水平方向的夾角∠ABC=∠ACB=30°,傘骨AB與AC水平方向的最大距離BC=2m,BC與AN交于點M,撐桿AN=2.2m,固定點O到地面的距離ON=1.6m.
(1)如圖②,當傘完全撐開并直立時,求點B到地面的距離.
(2)某日某時,為了增加遮擋斜射陽光的面積,將釣魚傘傾斜與鉛垂線HN成30°夾角,如圖③.
①求此時點B到地面的距離;
②若斜射陽光與BC所在直線垂直時,求BC在水平地面上投影的長度約是多少.(說明:![]() ≈1.732,結果精確到0.1m)
≈1.732,結果精確到0.1m)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學數學興趣小組在一次課外學習與探究中遇到一些新的數學符號,他們將其中某些材料摘錄如下:
對于三個實數a,b,c,用M{a,b,c}表示這三個數的平均數,用min{a,b,c}表示這三個數中最小的數.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.請結合上述材料,解決下列問題:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.請結合上述材料,解決下列問題:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市一研究機構為了了解![]() 歲年齡段市民對創建文明城市的關注程度,隨機選取了
歲年齡段市民對創建文明城市的關注程度,隨機選取了![]() 名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
名年齡在該范圍內的市民進行了調查,并將收集到的數據制成了尚不完整的頻數分布表、頻數分布直方圖和扇形統計圖,如下所示:
組別 | 年齡段 | 頻數(人數) |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
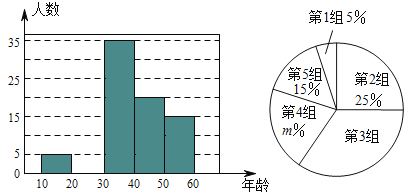
(1)請直接寫出![]() ,第
,第![]() 組人數在扇形統計圖中所對應的圓心角是 度;
組人數在扇形統計圖中所對應的圓心角是 度;
(2)請補全上面的頻數分布直方圖:
(3)假設該市現有![]() 歲的市民
歲的市民![]() 萬人,問
萬人,問![]() 歲年齡段的關注創建文明城市的人數約有多少?
歲年齡段的關注創建文明城市的人數約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】PM2.5是指大氣中直徑小于或等于2.5μm(0.0000025m)的顆粒物,含有大量有毒、有害物質,也稱可入肺顆粒物.將0.0000025用科學記數法表示為
A.25×10﹣7B.2.5×10﹣6C.0.25×10﹣5D.2.5×106
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com