
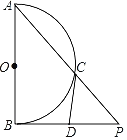
【題目】如圖,已知AB為半圓O的直徑,過點B作PB⊥OB,連接AP交半圓O于點C,D為BP上一點,CD是半圓O的切線.
(1)求證:CD=DP.
(2)已知半圓O的直徑為![]() ,PC=1,求CD的長.
,PC=1,求CD的長.
【答案】(1)證明見解析,(2)CD=![]() .
.
【解析】
(1)如圖1(見解析),連接OC,先根據圓的切線的性質得出![]() ,從而可得
,從而可得![]() ,再根據直角三角形的性質可得
,再根據直角三角形的性質可得![]() ,然后根據等腰三角形的性質可得
,然后根據等腰三角形的性質可得![]() ,從而可得
,從而可得![]() ,最后根據等腰三角形的性質即可得證;
,最后根據等腰三角形的性質即可得證;
(2)如圖2(見解析),連接OC、BC,先根據圓周角定理得出![]() ,再根據相似三角形的判定與性質可得
,再根據相似三角形的判定與性質可得![]() ,從而可求出
,從而可求出![]() ,然后在
,然后在![]() 中利用勾股定理可求出
中利用勾股定理可求出![]() ,最后根據角的和差、等腰三角形的性質可得
,最后根據角的和差、等腰三角形的性質可得![]() ,結合題(1)的結論可得
,結合題(1)的結論可得![]() ,由此即可得.
,由此即可得.
(1)如圖1,連接OC
∵CD是半圓O的切線
∴OC⊥CD,即![]()
∴![]()
∵PB⊥AB
∴![]()
∴![]()
![]()
又![]()
![]()
∴![]()
∴![]() ;
;
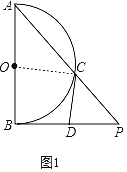
(2)如圖2,連接OC、BC
∵AB是半圓O的直徑
∴![]() ,
,![]()
∴![]()
又∵![]()
∴![]()
∴![]() ,即
,即![]()
∵![]()
∴![]()
解得![]() 或
或![]() (不符題意,舍去)
(不符題意,舍去)
∴![]()
在![]() 中,
中,![]()
由(1)得![]()
即![]()
∵![]()
∴![]()
∴![]()
∴![]()
由(1)知![]()
∴![]() .
.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源: 題型:
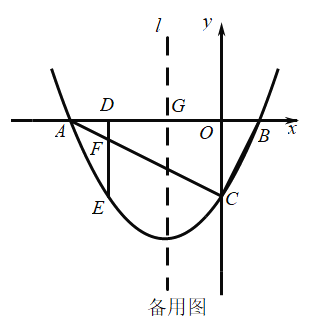
【題目】如圖,拋物線![]() 與
與![]() 軸負半軸交于點
軸負半軸交于點![]() ,與
,與![]() 軸正半軸交于點
軸正半軸交于點![]() ,與
,與![]() 軸負半軸交于點
軸負半軸交于點![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求點![]() 的坐標和拋物線的函數關系式;
的坐標和拋物線的函數關系式;
(2)點![]() 是
是![]() 上一點(不與點
上一點(不與點![]() 、
、![]() 重合),過點
重合),過點![]() 作
作![]() 軸的垂線,交拋物線于點
軸的垂線,交拋物線于點![]() ,交
,交![]() 于點
于點![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標;
的坐標;
(3)設拋物線的對稱軸![]() 交
交![]() 軸于點
軸于點![]() ,在(2)的條件下,點
,在(2)的條件下,點![]() 是拋物線對稱軸上一點,點
是拋物線對稱軸上一點,點![]() 是坐標平面內一點,是否存在點
是坐標平面內一點,是否存在點![]() 、
、![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是菱形?若存在,請求出點
為頂點的四邊形是菱形?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
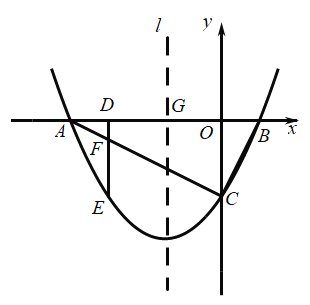
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小元步行從家去火車站,走到 6 分鐘時,以同樣的速度回家取物品,然后從家乘出租車趕往火車站,結果比預計步行時間提前了3 分鐘.小元離家路程S(米)與時間t(分鐘)之間的函數圖象如圖,從家到火車站路程是( )

A.1300 米B.1400 米C.1600 米D.1500 米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國古代數學著作(九章算術)中有如下問題:“今有人持金出五關,前關二而稅一.次關三而稅一,次關四而稅一,次關五而稅一,次關六而稅一,并五關所稅,適重一斤.”其意思為“今有人持金出五關,第![]() 關所收稅金為持金的
關所收稅金為持金的![]() ,第
,第![]() 關所收稅金為剩余金的
關所收稅金為剩余金的![]() ,第
,第![]() 關所收稅金為剩余金的
關所收稅金為剩余金的![]() ,第
,第![]() 關所收稅金為剩余金的
關所收稅金為剩余金的![]() ,第
,第![]() 關所收稅金為剩余金的
關所收稅金為剩余金的![]() ,
,![]() 關所收稅金之和,恰好重
關所收稅金之和,恰好重![]() 斤.”若設這個人原本持金
斤.”若設這個人原本持金![]() 斤,根據題意可列方程為__________ .
斤,根據題意可列方程為__________ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:有一組對角互補的四邊形叫做互補四邊形.
![]() 概念理解:
概念理解:
①在互補四邊形![]() 中,
中,![]() 與
與![]() 是一組對角,若
是一組對角,若![]() 則
則![]() _
_ ![]()
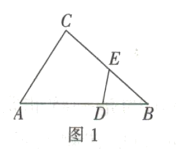
②如圖1,在![]() 中,點
中,點![]() 分別在邊
分別在邊![]() 上,且
上,且![]() 求證:四邊形
求證:四邊形![]() 是互補四邊形.
是互補四邊形.
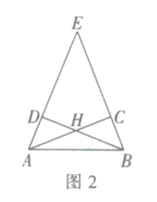
![]() 探究發現:如圖2,在等腰
探究發現:如圖2,在等腰![]() 中,
中,![]() 點
點![]() 分別在邊
分別在邊![]() 上,
上, ![]() 四邊形
四邊形![]() 是互補四邊形,求證:
是互補四邊形,求證:![]() .
.
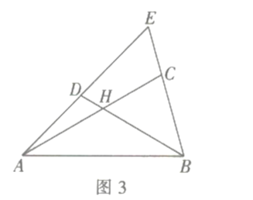
![]() 推廣運用:如圖3,在
推廣運用:如圖3,在![]() 中,點
中,點![]() 分別在邊
分別在邊![]() 上,
上,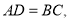 四邊形
四邊形![]() 是互補四邊形,若
是互補四邊形,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,點E是直線AB上的點,過點E的直線l交直線CD于點F,EG平分∠BEF交CD于點G.在直線l繞點E旋轉的過程中,圖中∠1,∠2的度數可以分別是( )
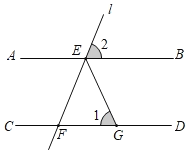
A.30°,110°B.56°,70°C.70°,40°D.100°,40°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,折疊矩形![]() ,具體操作:①點
,具體操作:①點![]() 為
為![]() 邊上一點(不與
邊上一點(不與![]() 、
、![]() 重合),把
重合),把![]() 沿
沿![]() 所在的直線折疊,
所在的直線折疊,![]() 點的對稱點為
點的對稱點為![]() 點;②過點
點;②過點![]() 對折
對折![]() ,折痕
,折痕![]() 所在的直線交
所在的直線交![]() 于點
于點![]() 、
、![]() 點的對稱點為
點的對稱點為![]() 點.
點.
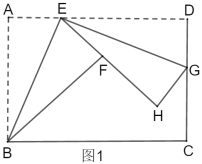
(1)求證:![]() ∽
∽![]() .
.
(2)若![]() ,
,![]() .
.
①點![]() 在移動的過程中,求
在移動的過程中,求![]() 的最大值.
的最大值.
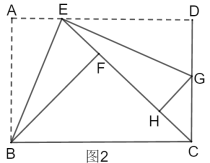
②如圖2,若點![]() 恰在直線
恰在直線![]() 上,連接
上,連接![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在如圖所示的網格中,有兩個完全相同的直角三角形紙片,如果把其中一個三角形紙片先橫向平移![]() 格,再縱向平移
格,再縱向平移![]() 格,就能使它的一條邊與另一個三角形紙片的一條邊重合,拼接成一個四邊形,那么
格,就能使它的一條邊與另一個三角形紙片的一條邊重合,拼接成一個四邊形,那么![]() 的結果( )
的結果( )

A.只有一個確定的值B.有兩個不同的值
C.有三個不同的值D.有三個以上不同的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠有甲、乙兩臺機器加工同一種零件,已知一小時甲加工的零件數與一小時乙加工的零件數的和為36個,甲加工80個零件與乙加工100個零件的所用時間相等.求甲、乙兩臺機器每小時分別加工零件多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com