
【題目】如圖,在△ABC中,∠ACB=90°,BC的垂直平分線DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)說明四邊形ACEF是平行四邊形;(2)當∠B滿足什么條件時,四邊形ACEF是菱形,并說明理由.

【答案】(1)、證明過程見解析;(2)、∠B=30°;理由見解析
【解析】
試題分析:(1)、根據DE垂直平分BC可得∠EDB=90°,得到DE∥AC,結合AF∥CE得到平行四邊形;(2)、根據DE垂直平分BC得到BE=EC,∠B=∠BCE,根據∠B=30°可得∠BCE=30°,∠AEC=60°,根據∠BCA=90°可得∠BAC=60°,則△ACE為正三角形,得到四邊形為菱形.
試題解析:(1)、∵ DE垂直平分BC ∴∠EDB=90° ∴ DE∥AC,即FE∥AC
由∵AF∥CE ∴四邊形ACEF是平行四邊形
(2)、當∠B=30°時,四邊形ACEF是菱形
理由:∵DE垂直平分BC ∴BE=EC ∴∠B=∠BCE ∵∠B=30° ∴∠BCE=30°
∴∠AEC=∠B+∠BCE=60° ∵∠BCA=90° ∴∠BAC=90°-∠B=60°
∴△ACE是等邊三角形 ∴AC=EC ∵四邊形ACEF是平行四邊形 ∴四邊形ACEF是菱形


科目:初中數學 來源: 題型:
【題目】為了預防“流感”,某學校對教室采用藥熏消毒法進行消毒,已知藥物燃燒時,室內每立方米空氣中的含藥量y(mg)與時間x(min)成正比例,藥物燃燒完后,y與x成反比例(如圖所示)。現測得藥物8min燃畢,此時室內空氣中每立方米的含藥量為6mg。研究表明,當空氣中每立方米的含藥量不低于3mg才有效,那么此次消毒的有效時間是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() (點
(點![]() 分別在
分別在![]() 軸的左右兩側)兩點,與
軸的左右兩側)兩點,與![]() 軸的正半軸交于點
軸的正半軸交于點![]() ,頂點為
,頂點為![]() ,已知點
,已知點![]() .
.
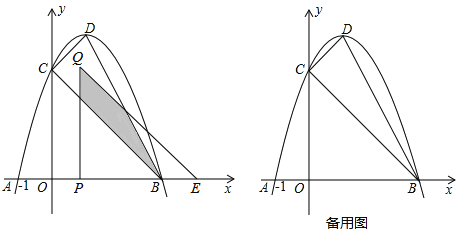
⑴.求點![]() 的坐標;
的坐標;
⑵.判斷△![]() 的形狀,并說明理由;
的形狀,并說明理由;
⑶.將△![]() 沿
沿![]() 軸向右平移
軸向右平移![]() 個單位(
個單位(![]() )得到△
)得到△![]() .△
.△![]() 與△
與△![]() 重疊部分(如圖中陰影)面積為
重疊部分(如圖中陰影)面積為![]() ,求
,求![]() 與
與![]() 的函數關系式,并寫出自變量
的函數關系式,并寫出自變量![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在□ABCD中,分別以AB、AD為邊向外作等邊△ABE,△ADF,延長CB交AE于點G,點G落在點A、E之間,連接EF、CF.則以下四個結論:①CG⊥AE;②△CDF≌△EBC;③∠CDF =∠EAF;④△ECF是等邊三角形.其中一定正確的是 .(把正確結論的序號都填上)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=2x﹣4的圖象與x、y軸交于B、A兩點,與y=![]() 的圖象交于點C,CD⊥x軸于點D,如果△CDB的面積:△AOB的面積=1:4,則k的值為 .
的圖象交于點C,CD⊥x軸于點D,如果△CDB的面積:△AOB的面積=1:4,則k的值為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】⊙O為△ABC的外接圓,過圓外一點P作⊙O的切線PA,且PA∥BC.

(1)如圖1,求證:△ABC為等腰三角形:
(2)如圖2,在AB邊上取一點E,AC邊上取一點F,直線EF交PA于點M,交BC的延長線于點N,若ME=FN,求證:AE=CF;
(3)如圖3,在(2)的條件下,連接OE、OF,∠EOF=120°,![]() ,EF=
,EF=![]() ,求⊙O的半徑長.
,求⊙O的半徑長.
查看答案和解析>>
科目:初中數學 來源: 題型:
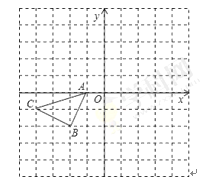
【題目】如圖所示的正方形網格中,△ABC的頂點均在格點上,請在所給直角坐標系中按要求畫圖和解答下列問題:
(1)將△ABC沿x軸翻折后再沿x軸向右平移1個單位,在圖中畫出平移后的△AB1C1。若△ABC內有一點P(a,b),則經過兩次變換后點P的坐標變為_____________
(2)作出△ABC關于坐標原點O成中心對稱的△A2B2C2.
(3) 若將△ABC繞某點逆時針旋轉90°后,其對應點分別為![]() ,則旋轉中心坐標為_________.
,則旋轉中心坐標為_________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com