
【題目】問題:如圖(1),在Rt△ACB中,∠ACB=90°,AC=CB,∠DCE=45°,試探究AD、DE、EB滿足的等量關系.
[探究發現]
小聰同學利用圖形變換,將△CAD繞點C逆時針旋轉90°得到△CBH,連接EH,由已知條件易得∠EBH=90°,∠ECH=∠ECB+∠BCH=∠ECB+∠ACD=45°.
根據“邊角邊”,可證△CEH≌ , 得EH=ED.
在Rt△HBE中,由定理,可得BH2+EB2=EH2 , 由BH=AD,可得AD、DE、EB之間的等量關系是 .
[實踐運用]
(1)如圖(2),在正方形ABCD中,△AEF的頂點E、F分別在BC、CD邊上,高AG與正方形的邊長相等,求∠EAF的度數;
(2)在(1)條件下,連接BD,分別交AE、AF于點M、N,若BE=2,DF=3,BM=2![]() ,運用小聰同學探究的結論,求正方形的邊長及MN的長.
,運用小聰同學探究的結論,求正方形的邊長及MN的長.
【答案】解:根據“邊角邊”,可證△CEH≌△CDE,得EH=ED.
在Rt△HBE中,由勾股定理,可得BH2+EB2=EH2 , 由BH=AD,可得AD、DE、EB之間的等量關系是AD2+EB2=DE2;故答案為:△CDE;勾股;AD2+EB2=DE2;
(1)在Rt△ABE和Rt△AGE中,![]() ,
,
∴Rt△ABE≌Rt△AGE(HL),
∴∠BAE=∠GAE,
同理,Rt△ADF≌Rt△AGF,
∴∠GAF=∠DAF,
∵四邊形ABCD是正方形,
∴∠BAD=90°,
∴∠EAF=![]() ∠BAD=45°;
∠BAD=45°;
(2)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,
∴BE=EG=2,DF=FG=3,則EF=5,
設AG=x,則CE=x﹣2,CF=x﹣3,
∵CE2+CF2=EF2 ,
∴(x﹣2)2+(x﹣3)2=52 ,
解這個方程,得x1=6,x2=﹣1(舍去),
∴AG=6,
∴BD=![]() ,
,
∴AB=6,
∵MN2=MB2+ND2
設MN=a,則![]() ,
,
所以a=![]() ,
,
即MN=![]() .
.
【解析】(1)根據正方形的性質和全等三角形的判定方法證明Rt△ABE≌Rt△AGE和Rt△ADF≌Rt△AGF,由全等三角形的性質即可求出∠EAF=![]() ∠BAD=45°;
∠BAD=45°;
(2)由(1)知,Rt△ABE≌Rt△AGE,Rt△ADF≌Rt△AGF,設AG=x,則CE=x﹣2,CF=x﹣3.因為CE2+CF2=EF2 , 所以(x﹣2)2+(x﹣3)2=52 . 解這個方程,求出x的值即可得到AG=6,在(2)中,MN2=MB2+ND2 , MN=a,![]() , 所以a=
, 所以a=![]() .即MN=
.即MN=![]() .
.
【考點精析】根據題目的已知條件,利用正方形的性質的相關知識可以得到問題的答案,需要掌握正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


科目:初中數學 來源: 題型:
【題目】為全面開展“陽光大課間”活動,某中學三個年級準備成立“足球”、“籃球”、“跳繩”、“踢毽”四個課外活動小組,學校體育組根據七年級學生的報名情況(每人限報一項)繪制了兩幅不完整的統計圖(如圖), 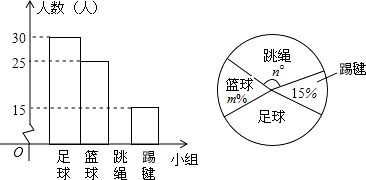
請根據以上信息,完成下列問題:
(1)m= , n= , 并將條形統計圖補充完整;
(2)根據七年級的報名情況,試問全校2000人中,大約有多少人報名參加足球活動小組?
(3)根據活動需要,從“跳繩”小組的二男二女四名同學中隨機選取兩人到“踢毽”小組參加訓練,請用列表或樹狀圖的方法計算恰好選中一男一女兩名同學的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABO中,已知點 ![]() 、B(﹣1,﹣1)、O(0,0),正比例函數y=﹣x圖象是直線l,直線AC∥x軸交直線l與點C.
、B(﹣1,﹣1)、O(0,0),正比例函數y=﹣x圖象是直線l,直線AC∥x軸交直線l與點C. 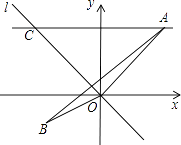
(1)C點的坐標為;
(2)以點O為旋轉中心,將△ABO順時針旋轉角α(90°≤α<180°),使得點B落在直線l上的對應點為B′,點A的對應點為A′,得到△A′OB′. ①∠α=;②畫出△A′OB′.
(3)寫出所有滿足△DOC∽△AOB的點D的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=5,BC=7,點E為BC上一動點,把△ABE沿AE折疊,當點B的對應點B′落在∠ADC的角平分線上時,則點B′到BC的距離為( )
A.1或2
B.2或3
C.3或4
D.4或5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D是BC的中點,點E、F分別是線段AD及其延長線上,且DE=DF,給出下列條件:①BE⊥EC;②BF∥EC;③AB=AC,從中選擇一個條件使四邊形BECF是菱形,并給出證明,你選擇的條件是___(只填寫序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D是等邊△ABC中BC邊的延長線上一點,且AC=CD,以AB為直徑作⊙O,分別交邊AC、BC于點E、點F
(1)求證:AD是⊙O的切線;
(2)連接OC,交⊙O于點G,若AB=4,求線段CE、CG與![]() 圍成的陰影部分的面積S.
圍成的陰影部分的面積S.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,坐標原點O為矩形ABCD的對稱中心,頂點A的坐標為(1,t),AB∥x軸,矩形A′B′C′D′與矩形ABCD是位似圖形,點O為位似中心,點A′,B′分別是點A,B的對應點,![]() =k.已知關于x,y的二元一次方程
=k.已知關于x,y的二元一次方程![]() (m,n是實數)無解,在以m,n為坐標記為(m,n)的所有的點中,若有且只有一個點落在矩形A′B′C′D′的邊上,則kt的值等于( )
(m,n是實數)無解,在以m,n為坐標記為(m,n)的所有的點中,若有且只有一個點落在矩形A′B′C′D′的邊上,則kt的值等于( )
A.![]()
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校分別于2012年、2014年隨機調查相同數量的學生,對數學課開展小組合作學習的情況進行調查(開展情況分為較少、有時、常常、總是四種),繪制成部分統計圖如下.請根據圖中信息,解答下列問題:
(1)a=%,b=%,“總是”對應陰影的圓心角為
(2)請你補全條形統計圖
(3)若該校2014年共有1200名學生,請你統計其中認為數學課“總是”開展小組合作學習的學生有多少名?
(4)相比2012年,2014年數學課開展小組合作學習的情況有何變化?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com