
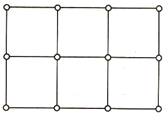
 如圖,在2×3矩形方格紙上,各個小正方形的頂點稱為格點,則以格點為頂點的等腰直角三角形的個數為________.
如圖,在2×3矩形方格紙上,各個小正方形的頂點稱為格點,則以格點為頂點的等腰直角三角形的個數為________. ACCD=
ACCD=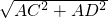 =
= ,然后進行分類討論:如等腰直角三角形ACB的邊長為1,每個小方格可得到4個這樣的三角形,則這樣的三角形的個數為6×4=24個;如等腰直角三角形ABE的邊長為
,然后進行分類討論:如等腰直角三角形ACB的邊長為1,每個小方格可得到4個這樣的三角形,則這樣的三角形的個數為6×4=24個;如等腰直角三角形ABE的邊長為 ,每兩個相鄰的小方格可得到4個這樣的三角形,則這樣的三角形的個數為7×2=14個;如等腰直角三角形DHE的邊長為2,每四個小方格組成的大正方形可得到4個這樣的三角形,則這樣的三角形的個數為2×4=8個;如等腰直角三角形ACB的邊長為
,每兩個相鄰的小方格可得到4個這樣的三角形,則這樣的三角形的個數為7×2=14個;如等腰直角三角形DHE的邊長為2,每四個小方格組成的大正方形可得到4個這樣的三角形,則這樣的三角形的個數為2×4=8個;如等腰直角三角形ACB的邊長為 ,矩形方格紙上上下兩邊各有兩個滿足條件的三角形的直角頂點,則這樣的三角形的個數為4個,然后把它們相加即可.
,矩形方格紙上上下兩邊各有兩個滿足條件的三角形的直角頂點,則這樣的三角形的個數為4個,然后把它們相加即可. AC,
AC,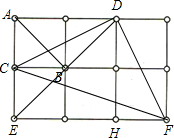 CD=
CD=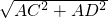 =
= ,
, 時(如等腰直角三角形ABE),這樣的三角形的個數為7×2=14個;
時(如等腰直角三角形ABE),這樣的三角形的個數為7×2=14個; 時(如等腰直角三角形ACB),這樣的三角形的個數為4個,
時(如等腰直角三角形ACB),這樣的三角形的個數為4個, 倍.
倍. 

科目:初中數學 來源: 題型:
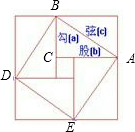
 7、三國時期的數學家趙爽,在其所著的《勾股圓方圖注》中記載用圖形的方法來解一元二次方程,四個相等的矩形(每一個矩形的面積都是35)拼成如圖所示的一個大正方形,利用所給的數據,能得到的方程是( )
7、三國時期的數學家趙爽,在其所著的《勾股圓方圖注》中記載用圖形的方法來解一元二次方程,四個相等的矩形(每一個矩形的面積都是35)拼成如圖所示的一個大正方形,利用所給的數據,能得到的方程是( )查看答案和解析>>
科目:初中數學 來源: 題型:
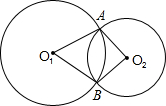 如圖,⊙O1與⊙O2相交于點A、B,順次連接O1、A、O2、B四點,得四邊形O1AO2B.
如圖,⊙O1與⊙O2相交于點A、B,順次連接O1、A、O2、B四點,得四邊形O1AO2B.查看答案和解析>>
科目:初中數學 來源: 題型:
 給出下列命題:①反比例函數y=
給出下列命題:①反比例函數y=| 2 |
| x |
| A、③④ | B、①②③ |
| C、②④ | D、①②③④ |
查看答案和解析>>
科目:初中數學 來源:2012年易學教育中考數學模擬試卷(19)(解析版) 題型:選擇題
 的圖象經過一、三象限,且y隨x的增大而減小;②對角線相等且有一個內角是直角的四邊形是矩形;③我國古代三國時期的數學家趙爽,創制了一幅“勾股圓方圖”,用形數結合得到方法,給出了勾股定理的詳細證明(如圖);④在同圓或等圓中,相等的弧所對的圓周角相等.其中正確的是( )
的圖象經過一、三象限,且y隨x的增大而減小;②對角線相等且有一個內角是直角的四邊形是矩形;③我國古代三國時期的數學家趙爽,創制了一幅“勾股圓方圖”,用形數結合得到方法,給出了勾股定理的詳細證明(如圖);④在同圓或等圓中,相等的弧所對的圓周角相等.其中正確的是( )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com