
 如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC,垂足為點F,連接DF,分析下列四個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\frac{\sqrt{2}}{2}$.其中正確的結論有( )
如圖,在矩形ABCD中,E是AD邊的中點,BE⊥AC,垂足為點F,連接DF,分析下列四個結論:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\frac{\sqrt{2}}{2}$.其中正確的結論有( )| A. | 4個 | B. | 3個 | C. | 2個 | D. | 1個 |
分析 ①正確.只要證明∠EAC=∠ACB,∠ABC=∠AFE=90°即可;
②正確.由AD∥BC,推出△AEF∽△CBF,推出$\frac{AE}{BC}$=$\frac{AF}{CF}$,由AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,推出$\frac{AF}{CF}$=$\frac{1}{2}$,即CF=2AF;
③正確.只要證明DM垂直平分CF,即可證明;
④正確.設AE=a,AB=b,則AD=2a,由△BAE∽△ADC,有 $\frac{b}{a}$=$\frac{2a}{b}$,即b=$\sqrt{2}$a,可得tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$.
解答 解:如圖,過D作DM∥BE交AC于N,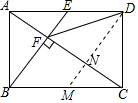 ∵四邊形ABCD是矩形,
∵四邊形ABCD是矩形,
∴AD∥BC,∠ABC=90°,AD=BC,
∵BE⊥AC于點F,
∴∠EAC=∠ACB,∠ABC=∠AFE=90°,
∴△AEF∽△CAB,故①正確;
∵AD∥BC,
∴△AEF∽△CBF,
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$,
∵AE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴$\frac{AF}{CF}$=$\frac{1}{2}$,
∴CF=2AF,故②正確;
∵DE∥BM,BE∥DM,
∴四邊形BMDE是平行四邊形,
∴BM=DE=$\frac{1}{2}$BC,
∴BM=CM,
∴CN=NF,
∵BE⊥AC于點F,DM∥BE,
∴DN⊥CF,
∴DM垂直平分CF,
∴DF=DC,故③正確;
設AE=a,AB=b,則AD=2a,
由△BAE∽△ADC,有 $\frac{b}{a}$=$\frac{2a}{b}$,即b=$\sqrt{2}$a,
∴tan∠CAD=$\frac{CD}{AD}$=$\frac{b}{2a}$=$\frac{\sqrt{2}}{2}$.故④正確;
故選A.
點評 本題主要考查了相似三角形的判定和性質,矩形的性質,圖形面積的計算以及解直角三角形的綜合應用,正確的作出輔助線構造平行四邊形是解題的關鍵.解題時注意:相似三角形的對應邊成比例.


 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{2}{x-1}$ | B. | $\frac{2}{x}$ | C. | $\frac{2}{x+1}$ | D. | 2(x+1) |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
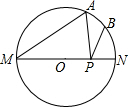 如圖,MN是⊙O的直徑,MN=4,∠AMN=30°,點B為弧AN的中點,點P是直徑MN上的一個動點,則PA+PB的最小值為( )
如圖,MN是⊙O的直徑,MN=4,∠AMN=30°,點B為弧AN的中點,點P是直徑MN上的一個動點,則PA+PB的最小值為( )| A. | 2 | B. | 2$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
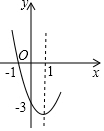 已知拋物線y=x2+bx+c的部分圖象如圖所示,若y<0,則x的取值范圍是( )
已知拋物線y=x2+bx+c的部分圖象如圖所示,若y<0,則x的取值范圍是( )| A. | -1<x<4 | B. | x<-1或x>3 | C. | x<-1或x>4 | D. | -1<x<3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
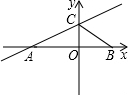 如圖,直線y=$\frac{1}{3}$x+1與x軸,y軸分別相交于點A,C兩點,點B在x軸上,連結BC,若∠ACB=135°,則點B的坐標為( )
如圖,直線y=$\frac{1}{3}$x+1與x軸,y軸分別相交于點A,C兩點,點B在x軸上,連結BC,若∠ACB=135°,則點B的坐標為( )| A. | (1,0) | B. | ($\sqrt{2}$,0) | C. | (2,0) | D. | ($\sqrt{5}$,0) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com