在Rt△ABC中,∠ACB=90°,∠A=30°,點D是AB的中點,DE⊥BC,垂足為點E,連接CD.
(1)如圖1,DE與BC的數量關系是______
【答案】
分析:(1)由∠ACB=90°,∠A=30°得到∠B=60°,根據直角三角形斜邊上中線性質得到DB=DC,則可判斷△DCB為等邊三角形,由于DE⊥BC,DE=
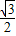
BC;
(2)根據旋轉的性質得到∠PDF=60°,DP=DF,易得∠CDP=∠BDF,則可根據“SAS”可判斷△DCP≌△DBF,則CP=BF,利用CP=BC-BP,DE=
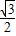
BC可得到BF+BP=
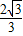
DE;
(3)與(2)的證明方法一樣得到△DCP≌△DBF得到CP=BF,而CP=BC+BP,則BF-BP=BC,所以BF-BP=

DE.
解答:解:(1)∵∠ACB=90°,∠A=30°,
∴∠B=60°,
∵點D是AB的中點,
∴DB=DC,
∴△DCB為等邊三角形,
∵DE⊥BC,
∴DE=
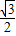
BC;
故答案為DE=

BC.
(2)BF+BP=
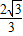
DE.理由如下:
∵線段DP繞點D逆時針旋轉60°,得到線段DF,
∴∠PDF=60°,DP=DF,
而∠CDB=60°,

∴∠CDB-∠PDB=∠PDF-∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中
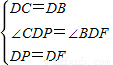
,
∴△DCP≌△DBF(SAS),
∴CP=BF,
而CP=BC-BP,
∴BF+BP=BC,
∵DE=

BC,
∴BC=
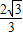
DE,
∴BF+BP=
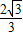
DE;
(3)如圖,
與(2)一樣可證明△DCP≌△DBF,
∴CP=BF,
而CP=BC+BP,
∴BF-BP=BC,
∴BF-BP=
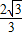
DE.
點評:本題考查了全等三角形的判定與性質:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的對應邊相等.也考查了等邊三角形的判定與性質以及含30度的直角三角形三邊的關系.

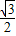 BC;
BC;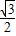 BC可得到BF+BP=
BC可得到BF+BP=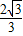 DE;
DE; DE.
DE.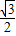 BC;
BC; BC.
BC.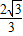 DE.理由如下:
DE.理由如下:
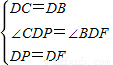 ,
, BC,
BC,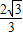 DE,
DE,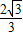 DE;
DE;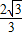 DE.
DE.

 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案