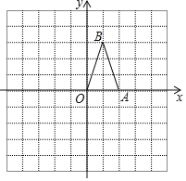
【題目】如圖，在平面直角坐標系中，已知點A（2，0），點B（1，3）．
（1）畫出將△OAB繞原點順時針旋轉90°后所得的△OA1B1，并寫出點A1，B1的坐標；
（2）畫出△OAB關于原點O的中心對稱圖形△OA2B2，并寫出點A2，B2的坐標．
【答案】（1）畫圖見解析；A1（0，﹣2），B1（3，﹣1）；（2）畫圖見解析；A2（﹣2，0），B2（﹣1，﹣3）.
【解析】
（1）根據題意所述的旋轉三要素找到各點的對應點，順次連接可得出旋轉后的圖形，再由順時針旋轉90°后點的橫坐標等于旋轉前點的縱坐標，縱坐標等于旋轉前點的橫坐標的相反數，即可得出A′、B′的坐標；（2）根據題意找到各點的對應點，順次連接可得出旋轉后的圖形，再由順時針旋轉后點的橫坐標等于旋轉前點的橫坐標的相反數，縱坐標等于旋轉前點的縱坐標的相反數，即可得A2、B2的坐標.
（1）如圖，△OA1B1即為所求，A1（0，﹣2），B1（3，﹣1）；
（2）如圖，△OA2B2即為所求，A2（﹣2，0），B2（﹣1，﹣3）；
暑假作業暑假快樂練西安出版社系列答案
新活力總動員暑系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=﹣ 
x+m（m＞0）的圖象與x軸、y軸分別交于點A，B，點C在線段OA上，點C的橫坐標為n，點D在線段AB上，且AD=2BD，將△ACD繞點D旋轉180°后得到△A1C1D．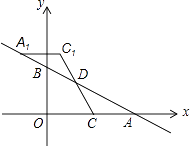
（1）若點C1恰好落在y軸上，試求 
的值；
（2）當n=4時，若△A1C1D被y軸分得兩部分圖形的面積比為3：5，求該一次函數的解析式．
查看答案和解析>>
科目：初中數學 來源： 題型：
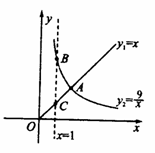
【題目】函數 yl= x ( x ≥0 ) , 
（ x > 0 ）的圖象如圖所示，則結論： ① 兩函數圖象的交點A的坐標為（3 ,3 ) ② 當 x > 3 
時， ③ 當 x ＝1時， BC = 8
④ 當 x 逐漸增大時， yl 隨著 x 的增大而增大，y2隨著 x 的增大而減小．其中正確結論的序號是＿ .
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】你知道什么是“低碳生活”嗎？“低碳生活”是指人們生活中盡量減少所耗能量，從而降低碳（特別是二氧化碳）的排放量的一種生活方式．
（1）如果用x（L）表示耗油量，用y（kg）表示開私家車的二氧化碳排放量，則y與x之間的關系式可表示為___________；
（2）在上述關系式中，耗油量每增加1L，二氧化碳排放量增加________kg．當耗油量從10L增加到100L時，二氧化碳排放量從________kg增加到________kg；
（3）小穎家本月家居用電的耗電量約為90kwh、開私家車的耗油量約為70L、天然氣使用量約20m、自來水使用量約6噸，請你計算一下小穎家本月這幾項的二氧化碳排放總量；
（4）你打算從哪些小事做起踐行低碳生活？請直接寫出兩條．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】分如圖，在ABCD中，點E、F分別是AD、BC的中點，分別連接BE、DF、BD．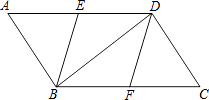
（1）求證：△AEB≌△CFD；
（2）若四邊形EBFD是菱形，求∠ABD的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，點E是邊長為1的正方形ABCD的邊AB上任意一點（不含A，B），過B，C，E三點的圓與BD相交于點F，與CD相交于點G，與∠ABC的外角平分線相交于點H．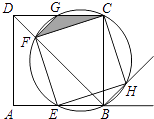
（1）求證：四邊形EFCH是正方形；
（2）設BE=x，△CFG的面積為y，求y與x的函數關系式，并求y的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，線段AB在x軸上點A，B的坐標分別為（﹣1，0），（3，0），現同時將點A，B分別向上平移2個單位，再向右平移1個單位，分別得到點A，B的對應點C，D，連接AC，BD，CD．得平行四邊形ABDC
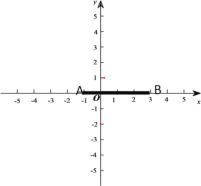
（1）補全圖形，直接寫出點C，D的坐標；
（2）若在y軸上存在點M，連接MA，MB，使S△MAB=S四邊形ABDC，求出點M的坐標．
（3）若點P在直線BD上運動，連接PC，PO．請畫出圖形，探索∠CPO、∠DCP、∠BOP的數量關系并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
