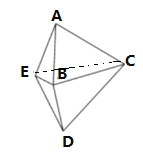
【題目】如圖，線段
，
的垂直平分線交于點
，且
，
，則
的度數為 ________ ．
【答案】
【解析】
連接CE，由線段
，
的垂直平分線交于點
，得CA=CB，CE=CD，ACB=∠ECD=36°，進而得∠ACE=∠BCD，易證ACEBCD，設∠AEC=∠BDC=x，得則∠BDE=72°-x，∠CEB=92°-x，BDE中，∠EBD=128°，根據三角形內角和定理，即可得到答案．
連接CE，
∵線段，的垂直平分線交于點，
∴CA=CB，CE=CD，
∵
=∠DEC，
∴∠ACB=∠ECD=36°，
∴∠ACE=∠BCD，
在ACE與BCD中，
∵
，
∴ACEBCD（SAS），
∴∠AEC=∠BDC，
設∠AEC=∠BDC=x，則∠BDE=72°-x，∠CEB=92°-x，
∴∠BED=∠DEC-∠CEB=72°-（92°-x）=x-20°，
∴在BDE中，∠EBD=180°-（72°-x）-（x-20°）=128°．
故答案是：．
閱讀快車系列答案科目：初中數學 來源： 題型：
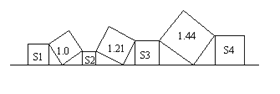
【題目】如圖，在直線l上依次擺放著七個正方形，已知斜放置的三個正方形的面積分別為1.0，1.21，1.44，正放置的四個正方形的面積為S1、S2、S3、S4，則S1+S2+S3+S4= ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場出售一批進價為2元的賀卡,在營運中發現此商品的日銷價x(單位:元)與銷售量y(單位:張)之間有如下關系:
x/元 | 3 | 4 | 5 | 6 |
y/張 | 20 | 15 | 12 | 10 |
(1)猜測并確定y與x的函數關系式.
(2)當日銷售單價為10元時,賀卡的日銷售量是多少張?
(3)設此卡的利潤為W元,試求出W與x之間的函數關系式,若物價部門規定此卡的銷售單價不能超過10元,試求出當日銷售單價為多少元時,每天獲得的利潤最大并求出最大的利潤.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y=kx+b（k、b為常數，k≠0）的圖象與x軸、y軸分別交于A、B兩點，且與反比例函數y=
（n為常數，且n≠0）的圖象在第二象限交于點C．CD⊥x軸，垂足為D，若OB=2OA=3OD=12．
（1）求一次函數與反比例函數的解析式；
（2）記兩函數圖象的另一個交點為E，求△CDE的面積；
（3）直接寫出不等式kx+b≤的解集．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料，完成（1）-（3）題：數學課上，老師出示了這樣一道題：如圖1，點
是正
邊
上一點以
為邊做正
，連接
.探究線段
與的數量關系，并證明.同學們經過思考后，交流了自已的想法：
小明：“通過觀察和度量，發現
與
相等.”
小偉：“通過全等三角形證明，再經過進一步推理，可以得到線段
平分
.”......
老師：“保留原題條件，連接
，
是
的延長線上一點，
（如圖2），如果
，可以求出
、
、
三條線段之間的數量關系.”
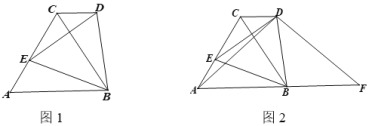
（1）求證
；
（2）求證線段平分；
（3）探究、、三條線段之間的數量關系，并加以證明.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC三個頂點的坐標分別為A（1，1），B（4，2），C（3，4）.
(1) 請畫出△ABC向左平移5個單位長度后得到的△A
B
C
；
(2) 請畫出△ABC關于原點對稱的△A
B
C
；
(3) 在
軸上求作一點P，使△PAB的周長最小，請畫出△PAB，并直接寫出P的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，一次函數y= -3x+6的圖象與
軸、
軸分別交于
、
兩點．
（1）將直線
向左平移1個單位長度，求平移后直線的函數關系式；
（2）求出平移過程中，直線在第一象限掃過的圖形的面積．
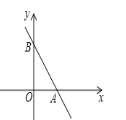
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某青春黨支部在精準扶貧活動中，給結對幫扶的貧困家庭贈送甲、乙兩種樹苗讓其栽種．已知乙種樹苗的價格比甲種樹苗貴10元，用480元購買乙種樹苗的棵數恰好與用360元購買甲種樹苗的棵數相同．
（1）求甲、乙兩種樹苗每棵的價格各是多少元？
（2）在實際幫扶中，他們決定再次購買甲、乙兩種樹苗共50棵，此時，甲種樹苗的售價比第一次購買時降低了10%，乙種樹苗的售價不變，如果再次購買兩種樹苗的總費用不超過1500元，那么他們最多可購買多少棵乙種樹苗？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=
x2+bx+c的圖象交x軸于A、D兩點，并經過B點，已知A點坐標是（2，0），B點坐標是（8，6）．
（1）求二次函數的解析式；
（2）求函數圖象的頂點坐標及D點的坐標；
（3）二次函數的對稱軸上是否存在一點C，使得△CBD的周長最小？若C點存在，求出C點的坐標；若C點不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com