
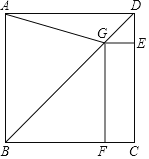
【題目】如圖,在正方形ABCD中,點G在對角線BD上![]() 不與點
不與點![]() 重合
重合![]() 于點
于點![]() 于點F,連結AG.
于點F,連結AG.
![]() 寫出線段
寫出線段![]() 長度之間的數量關系,并說明理由;
長度之間的數量關系,并說明理由;
![]() 若正方形ABCD的邊長為
若正方形ABCD的邊長為![]() ,求線段BG的長.
,求線段BG的長.
【答案】(1)結論: ![]() ,理由見解析;(2)
,理由見解析;(2)![]() .
.
【解析】試題分析:(1)結論: ![]() 只要證明GA=GC,四邊形EGFC是矩形,推出CF=GE,在Rt△GFC中,利用勾股定理即可證明;
只要證明GA=GC,四邊形EGFC是矩形,推出CF=GE,在Rt△GFC中,利用勾股定理即可證明;
(2)作BN⊥AG于N,在BN上截取一點M,使得AM=BM.設AN=x.易證![]()
![]() 在Rt△ABN中,根據
在Rt△ABN中,根據![]() 得
得![]() 解得
解得![]() 推出
推出![]() 再根據
再根據![]() 即可解決問題;
即可解決問題;
試題解析:(1)結論: ![]()
理由:連接CG.
∵四邊形ABCD是正方形,
∴A、C關于對角線BD對稱,
∵點G在BD上,
∴GA=GC,
∵GE⊥DC于點E,GF⊥BC于點F,
![]()
∴四邊形EGFC是矩形,
∴CF=GE,
在Rt△GFC中, ![]()
![]()

(2)作BN⊥AG于N,在BN上截取一點M,使得AM=BM.設AN=x.
![]()
![]()
![]()
![]()
在Rt△ABN中, ![]()
![]() 解得
解得![]()
![]()
![]()


 發散思維新課堂系列答案
發散思維新課堂系列答案科目:初中數學 來源: 題型:
【題目】我們給出如下定義:若一個四邊形中存在相鄰兩邊的平方和等于一條對角線的平方,則稱這個四邊形為勾股四邊形,這兩條相鄰的邊稱為這個四邊形的勾股邊.
(1)如圖①,已知格點(小正方形的頂點)O(0,0),A(3,0),B(0,4),請你畫出以格點為頂點,OA,OB為勾股邊且對角線相等的勾股四邊形OAMB;


(2)如圖②,將△ABC繞頂點B按順時針方向旋轉60°,得到△DBE,連接AD,DC,∠DCB=30°,求證:DC2+BC2=AC2,即四邊形ABCD是勾股四邊形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個矩形紙片OACB,將該紙片放置在平面直角坐標系中,點A(11,0),點B(0,6),點P為BC邊上的動點(點P不與點B,C重合),經過點O、P折疊該紙片,得點B′和折痕OP(如圖①)經過點P再次折疊紙片,使點C落在直線PB′上,得點C′和折痕PQ(如圖②),當點C′恰好落在OA上時,點P的坐標是 . 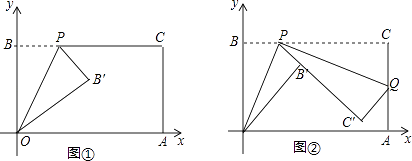
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為提高居民的節水意識,向陽小區開展了“建設節水型社區,保障用水安全”為主題的節水宣傳活動.小瑩同學積極參與小區的宣傳活動,并對小區300戶家庭用水情況進行了抽樣調查.她在300戶家庭中隨機調查了50戶家庭5月份的用水量,結果如圖所示.把圖中每組用水量的值用該組的中間值(如0~6的中間值為3)來代替,估計該小區5月份的用水量.
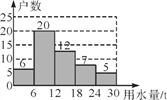
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,關于 x,y 的方程組![]() 的解滿足 x<0,y>0.
的解滿足 x<0,y>0.
(1)x= ,y= (用含 a 的代數式表示);
(2)求 a 的取值范圍;
(3)若 2x8y=2m,用含有 a 的代數式表示 m,并求 m 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC 中,∠A=90°,AB=AC=![]() +1,P 是△ABC 內一個動點,PD⊥AB、PE⊥AC、PF⊥BC,垂足分別為 D、E、F,且 PD+PE=PF.則點 P 運動所形成的圖形的長度是__________.
+1,P 是△ABC 內一個動點,PD⊥AB、PE⊥AC、PF⊥BC,垂足分別為 D、E、F,且 PD+PE=PF.則點 P 運動所形成的圖形的長度是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE與AC交于點M,EF與AC交于點N,動點P從點A出發沿AB以每秒1個單位長的速度向點B勻速運動,伴隨點P的運動,矩形PEFG在射線AB上滑動;動點K從點P出發沿折線PE﹣﹣EF以每秒1個單位長的速度勻速運動.點P、K同時開始運動,當點K到達點F時停止運動,點P也隨之停止.設點P、K運動的時間是t秒(t>0). 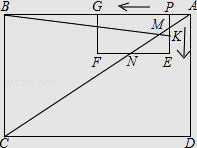
(1)當t=1時,KE= , EN=;
(2)當t為何值時,△APM的面積與△MNE的面積相等?
(3)當點K到達點N時,求出t的值;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作與探究 探索:在如圖1至圖3中,△ABC的面積為a .
(1)如圖1, 延長△ABC的邊BC到點D,使CD=BC,連結DA.若△ACD的面積為S1,則S1=________(用含a的代數式表示);




(2)如圖2,延長△ABC的邊BC到點D,延長邊CA到點E,使CD=BC,AE=CA,連結DE.若△DEC的面積為S2,則S2= (用含a的代數式表示);
(3)在圖2的基礎上延長AB到點F,使BF=AB,連結FD,FE,得到△DEF(如圖3).若陰影部分的面積為S3,則S3=__________(用含a的代數式表示).
發現:像上面那樣,將△ABC各邊均順次延長一倍,連結所得端點,得到△DEF(如圖3),此時,我們稱△ABC向外擴展了一次.可以發現,擴展一次后得到的△DEF的面積是原來△ABC面積的_____倍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com