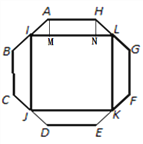
【題目】如圖，正八邊形ABCDEFGH的邊長為a，I、J、K、L分別是各自所在邊的中點，且四邊形IJKL是正方形，則正方形IJKL的邊長為________（用含a的代數式表示）．
【答案】
【解析】分析：過點A作AM⊥IL于點M，過點H作HN⊥IL與點N，可得四邊形AMNH為矩形，根據正八邊形的性質可得∠BAH=135°，由此可得∠BAM=45°，在等腰直角三角形AIM中，AI=
，可求得AM=IM=
，同理求得HN=LN=，所以IL=IM+MN+LN=IM+AH+LN=+a+=.
詳解：
過點A作AM⊥IL于點M，過點H作HN⊥IL與點N，可得四邊形AMNH為矩形，
∵八邊形ABCDEFGH為正八邊形，
∴∠BAH=135°，
∵∠HAM=90°，
∴∠BAM=45°，
在等腰直角三角形AIM中，AI=
∴AM=IM=；
同理求得HN=LN=，
∴IL=IM+MN+LN=IM+AH+LN=+a+=.
故答案為： .
備戰中考寒假系列答案科目：初中數學 來源： 題型：
【題目】小劉同學在一次課外活動中，用硬紙片做了兩個直角三角形，在
中，
，
，
；在
中，
，
，
.圖①是小劉同學所做的一個數學探究：他將的直角邊
與的斜邊
重合在一起，并將沿方向移動.在移動過程中，
、
兩點始終在邊上（移動開始時點與點
重合）.
（1）在沿方向移動的過程中，小劉發現：
、
兩點間的距離逐漸 ；連接
后，
的度數逐漸 .（填“不變”、“變大”或“變小”）；
（2）小劉同學經過進一步地研究，編制了如下問題：
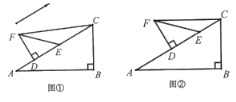
問題①：如圖②，當、
的連線與
平行時，求平移距離
的長；
問題②：如圖③，在的移動過程中，
的值是否為定值？如果是，請求出此定值；如果不是，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】問題呈現：如圖1，點E、F、G、H分別在矩形ABCD的邊AB、BC、CD、DA上，AE=DG，求證：2S四邊形EFGH=S矩形ABCD．（S表示面積）
實驗探究：某數學實驗小組發現：若圖1中AH≠BF，點G在CD上移動時，上述結論會發生變化，分別過點E、G作BC邊的平行線，再分別過點F、H作AB邊的平行線，四條平行線分別相交于點A1、B1、C1、D1，得到矩形A1B1C1D1．
如圖2，當AH＞BF時，若將點G向點C靠近（DG＞AE），經過探索，發現：2S四邊形EFGH=S矩形ABCD+
．
如圖3，當AH＞BF時，若將點G向點D靠近（DG＜AE），請探索S四邊形EFGH、S矩形ABCD與之間的數量關系，并說明理由．
遷移應用：
請直接應用“實驗探究”中發現的結論解答下列問題：
如圖4，點E、F、G、H分別是面積為25的正方形ABCD各邊上的點，已知AH＞BF，AE＞DG，S四邊形EFGH=11，HF=
，求EG的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是正方形，直線l1、l2、l3分別通過A、B、C三點，且l1∥l2∥l3，若l1與l2的距離為6，正方形ABCD的面積等于100，l2與l3的距離為（ ）
A. 8B. 10C. 9D. 7
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知點A（1，0），B（0，2），以AB為邊在第一象限內作正方形ABCD，直線CD與y軸交于點G，再以DG為邊在第一象限內作正方形DEFG，若反比例函數
的圖像經過點E，則k的值是 （ ）
（A）33 （B）34 （C）35 （D）36
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市在藝術節中組織中小學校文藝匯演，甲、乙兩所學校共92名學生
其中甲校學生多于乙校學生，且甲校學生不足90名
，現準備統一購買服裝參加演出，下表是某服裝廠給出的演出服裝價格表：
購買服裝的套數 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服裝的價格 | 60元 | 50元 | 40元 |
如果兩所學校單獨購買服裝，一共應付5000元
（1）甲、乙兩校各有多少名學生準備參加匯演？
（2）如果甲、乙兩校聯合起來購買服裝，那么比各自購買服裝共可以節省多少錢？
（3）如果甲校有10名學生被調去參加書法繪畫比賽不能參加演出，請你為兩校設計購買服裝方案，并說明哪一種最省錢．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知菱形ABCD的對角線相交于點O，延長AB至點E，使BE=AB，連接CE．
（1）求證：BD=EC；
（2）若∠E=50°，求∠BAO的大小．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】簡答題：
（1）當
為何值時，關于
的方程
是一元二次方程？
（2）已知關于的一元二次方程
有一個根是0，求的值．
（3）在第（2）題中，如果要使已知方程有一個根是l，那么m應該等于什么數？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】天空中有一個靜止的廣告氣球C，從地面A點測得C點的仰角為45°，從地面B測得仰角為60°，已知AB=20米，點C和直線AB在同一鉛垂平面上，求氣球離地面的高度.（結果精確到0.1米）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com