
【題目】如圖為正三角形ABC與正方形DEFG的重疊情形,其中D、E兩點分別在AB、BC上,且BD=BE.若AC=18,GF=6,則F點到AC的距離為何?( ) 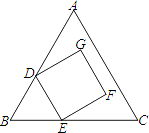
A.2
B.3
C.12﹣4 ![]()
D.6 ![]() ﹣6
﹣6
【答案】D
【解析】解:如圖,過點B作BH⊥AC于H,交GF于K, 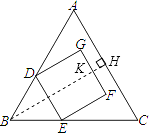
∵△ABC是等邊三角形,
∴∠A=∠ABC=60°,
∵BD=BE,
∴△BDE是等邊三角形,
∴∠BDE=60°,
∴∠A=∠BDE,
∴AC∥DE,
∵四邊形DEFG是正方形,GF=6,
∴DE∥GF,
∴AC∥DE∥GF,
∴KH=18× ![]() ﹣6×
﹣6× ![]() ﹣6=9
﹣6=9 ![]() ﹣3
﹣3 ![]() ﹣6=6
﹣6=6 ![]() ﹣6,
﹣6,
∴F點到AC的距離為6 ![]() ﹣6.
﹣6.
故選D.
【考點精析】根據題目的已知條件,利用等邊三角形的性質和正方形的性質的相關知識可以得到問題的答案,需要掌握等邊三角形的三個角都相等并且每個角都是60°;正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
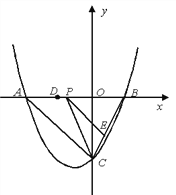
【題目】如圖,拋物線y=![]() x2+bx+c與y軸交于點C(0,-4),與x軸交于A、B,且點B的坐標為(2,0).
x2+bx+c與y軸交于點C(0,-4),與x軸交于A、B,且點B的坐標為(2,0).
(1)求該拋物線的解析式;
(2) 若點P是AB上的一動點,過點P作PE∥AC,交BC于E,連接CP,求△PCE面積的最大值;
(3) 若點D為OA的中點,點M是線段AC上一點,且△OMD是等腰三角形,求M點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據下面的點陣圖形和與之對應的等式,探究其中的規律:
(1) 請你在④和⑤后面的橫線上分別寫出對應的等式:
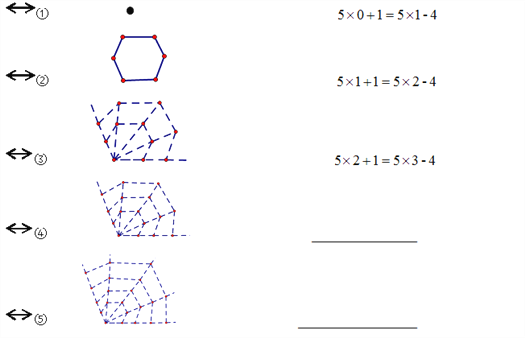
(2)通過猜想,寫出與第n個點陣圖形相對應的等式.
(3)求:點的個數等于96的點陣圖形是第幾個.
(4)判斷:是否存在點的個數等于2018的點陣圖形,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=2,∠BAD=60°,E是邊AD的中點,M是邊AB上任一點(不與點A重合),延長ME交CD的延長線與點N,連接MD,AN. 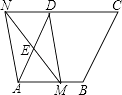
(1)求證:四邊形AMDN是平行四邊形;
(2)當AM=時,四邊形AMDN是矩形(直接寫答案即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在3×3方格上做填字游戲,要求每行每列及對角線上三個方格中的數字和都等于S,又填在圖中三格中的數字如圖,若要能填成,則( )
10
8 13
A.S=24 B.S=30 C.S=31 D.S=39
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了擴大內需,讓惠于農民,豐富農民的業余生活,鼓勵送彩電下鄉,國家決定對購買彩電的農戶實行政府補貼.規定每購買一臺彩電,政府補貼若干元,經調查某商場銷售彩電臺數y(臺)與補貼款額x(元)之間大致滿足如圖①所示的一次函數關系.隨著補貼款額x的不斷增大,銷售量也不斷增加,但每臺彩電的收益Z(元)會相應降低且Z與x之間也大致滿足如圖②所示的一次函數關系.
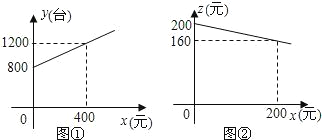
(1)在政府未出臺補貼措施前,該商場銷售彩電的總收益額為多少元?
(2)在政府補貼政策實施后,分別求出該商場銷售彩電臺數y和每臺家電的收益z與政府補貼款額x之間的函數關系式;
(3)要使該商場銷售彩電的總收益w(元)最大,政府應將每臺補貼款額x定為多少并求出總收益w的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
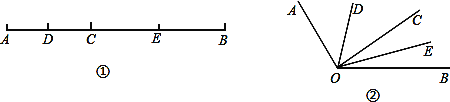
【題目】如圖①,已知線段AB=12cm,點C為AB上的一個動點,點D、E分別是AC和BC的中點.
(1)若AC=4cm,求DE的長;
(2)試利用“字母代替數”的方法,說明不論AC取何值(不超過12cm),DE的長不變;
(3)知識遷移:如圖②,已知∠AOB=120°,過角的內部任一點C畫射線OC,若OD、OE分別平分∠AOC和∠BOC,試說明∠DOE的度數與射線OC的位置無關.
查看答案和解析>>
科目:初中數學 來源: 題型:
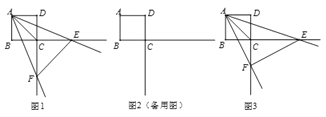
【題目】已知正方形ABCD的邊長為4,一個以點A為頂點的45°角繞點A旋轉,角的兩邊分別與邊BC、DC的延長線交于點E、F,連接EF。設CE=a,CF=b。
(1)如圖1,當∠EAF被對角線AC平分時,求a、b的值;
(2)當△AEF是直角三角形時,求a、b的值;
(3)如圖3,探索∠EAF繞點A旋轉的過程中a、b滿足的關系式,并說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com