Question

解不等式組，并把它們的解集在數軸上表示出來．
（1）6x≤7x-2
（2）

2x-1

3

-4＜-

x+4

2

（3）

x-3 2 +3≥x 1-3(x-1)＜8-x

（4）

2x-1＞0 1 2 (x+4)＜3

．

Answer 1

分析：（1）移項合并，然后系數化1，即可求得答案．在數軸上表示時：注意此題為實心點，方向向右．
（2）首先去分母，然后去括號，移項合并，系數化1，即可求得答案．在數軸上表示時：注意此題為空心點，方向向左．
（3）首先分別解兩個一元一次不等式，然后求得其解集即可．注意在數軸上表示時：注意若邊界點含于解集為實心點，不含于解集即為空心點，此題-2處為空心點，3處為實心點．
（4）首先分別解兩個一元一次不等式，然后求得其解集即可．注意在數軸上表示時：注意若邊界點含于解集為實心點，不含于解集即為空心點，此題均是空心點．

解答：解：（1）移項合并得：-x≤-2，
系數化1得：x≥2；
∴原不等式的解集為：x≥2；
在數軸上表示為：


（2）去分母得：2（2x-1）-24＜-3（x+4），
去括號得：4x-2-24＜-3x-12，
移項合并得：7x＜14，
系數化1，得：x＜2；
∴原不等式的解集為：x＜2；
在數軸上表示為：


（3）∵

x-3 2 +3≥x   ① 1-3(x-1)＜8-x  ②

，
由①得：x≤3，
由②得：x＞-2，
∴原不等式組的解集為：-2＜x≤3；
在數軸上表示為：


（4）∵

2x-1＞0  ① 1 2 (x+4)＜3 ②

，
由①得：x＞

1

2

，
由②得：x＜2，
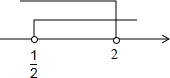
∴原不等式組的解集為：

1

2

＜x＜2．
在數軸上表示為：

點評：此題考查了一元一次不等式（組）的解法．注意解不等式依據不等式的基本性質，特別是在系數化為1這一個過程中要注意不等號的方向的變化．去分母的過程中注意不能漏乘沒有分母的項．用數軸表示不等式的解集時：注意時實心點還是空心點，方向是向右還是向左．