
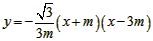 的頂點為M,拋物線交x軸于A、B兩點,交y軸正半軸于D點,以AB為直徑作圓,圓心為C,定點E的坐標為(-3,0),連接ED(m>0)。
的頂點為M,拋物線交x軸于A、B兩點,交y軸正半軸于D點,以AB為直徑作圓,圓心為C,定點E的坐標為(-3,0),連接ED(m>0)。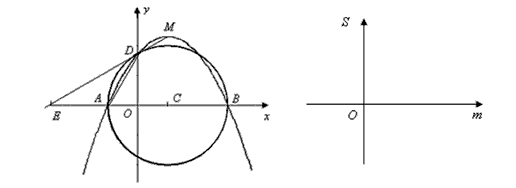
解:(1)A(-m,0),B(3,0),D(0,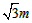 )。 )。 |
|
| (2)設直線ED的解析式為, 將E(-3,0),D(0,  )代入得: )代入得: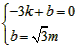 ,解得 ,解得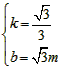 , ,∴直線ED的解析式為 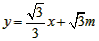 , ,將 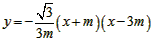 化為頂點式: 化為頂點式: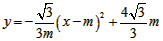 , , ∴頂點M的坐標為(  ), ),代入 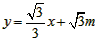 得:m2=m, 得:m2=m,∵m>0, ∴m=1, ∴當m=1時,M點在直線DE上, 連接CD,C為AB中點,此時,C點坐標為(1,0),D點坐標為(0, 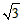 ), ),∴OD= 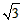 ,OC=1, ,OC=1,∴CD= 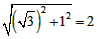 , ,又∵OE=3, ∴DE2=OD2+OE2= 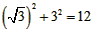 , ,又EC2=16,CD2=4, ∴CD2+DE2=EC2, ∴∠FDC=90°, 由CD=2知,D點在圓上, ∴直線ED與⊙C相切; |
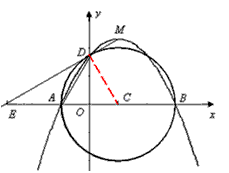 |
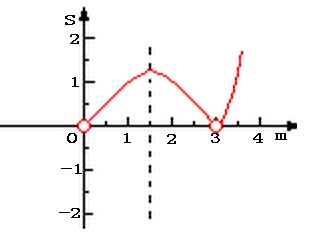
(3)當0<m<3時,S△AED=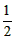 AE·OD= AE·OD=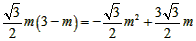 , ,當m>3時,S△AED= 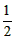 AE·OD= AE·OD=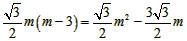 , ,S關于m的示意圖如右: |
 |


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:初中數學 來源: 題型:
| 1 | 2 |
 點.
點.查看答案和解析>>
科目:初中數學 來源: 題型:
 21、如圖,拋物線的頂點為A(1,-4),且過點B(3,0).
21、如圖,拋物線的頂點為A(1,-4),且過點B(3,0).查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•河南)如圖,拋物線的頂點為P(-2,2),與y軸交于點A(0,3).若平移該拋物線使其頂點P沿直線移動到點P′(2,-2),點A的對應點為A′,則拋物線上PA段掃過的區域(陰影部分)的面積為
(2013•河南)如圖,拋物線的頂點為P(-2,2),與y軸交于點A(0,3).若平移該拋物線使其頂點P沿直線移動到點P′(2,-2),點A的對應點為A′,則拋物線上PA段掃過的區域(陰影部分)的面積為查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•峨眉山市二模)已知,如圖,拋物線的頂點為C(1,-2),直線y=kx+m與拋物線交于A、B兩點,其中OA=3,B點在y軸上.點P為線段AB上的一個動點(點P與點A、B不重合),過點P且垂直于x軸的直線與這條拋物線交于點E.
(2013•峨眉山市二模)已知,如圖,拋物線的頂點為C(1,-2),直線y=kx+m與拋物線交于A、B兩點,其中OA=3,B點在y軸上.點P為線段AB上的一個動點(點P與點A、B不重合),過點P且垂直于x軸的直線與這條拋物線交于點E.查看答案和解析>>
科目:初中數學 來源: 題型:
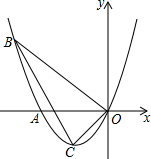 (2013•鄂爾多斯)如圖,拋物線的頂點為C(-1,-1),且經過點A、點B和坐標原點O,點B的橫坐標為-3.
(2013•鄂爾多斯)如圖,拋物線的頂點為C(-1,-1),且經過點A、點B和坐標原點O,點B的橫坐標為-3.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com