
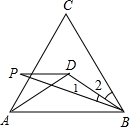
 如圖所示,D為等邊△ABC內一點,且BD=AD,BP=AB,∠1=∠2,則∠P=
如圖所示,D為等邊△ABC內一點,且BD=AD,BP=AB,∠1=∠2,則∠P=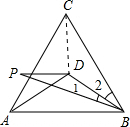 解:如圖,連接CD,
解:如圖,連接CD,| 1 |
| 2 |
| 1 |
| 2 |


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:初中數學 來源: 題型:
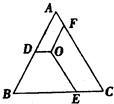 22、如圖所示,O為等邊△ABC內任意一點,OD∥BC,OE∥AC,OF∥AB,并且D、E、F分別在AB、BC、AC上,求證:OD+OE+OF=BC.
22、如圖所示,O為等邊△ABC內任意一點,OD∥BC,OE∥AC,OF∥AB,并且D、E、F分別在AB、BC、AC上,求證:OD+OE+OF=BC.查看答案和解析>>
科目:初中數學 來源: 題型:
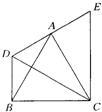 21、如圖所示,△ABC為等邊三角形,以AB為邊向外作△ABD,使∠ADB=120°,然后把△BCD繞著點C按順時針方向旋轉60°得到△ACE,如圖所示,已知BD=5,AD=3.
21、如圖所示,△ABC為等邊三角形,以AB為邊向外作△ABD,使∠ADB=120°,然后把△BCD繞著點C按順時針方向旋轉60°得到△ACE,如圖所示,已知BD=5,AD=3.查看答案和解析>>
科目:初中數學 來源: 題型:
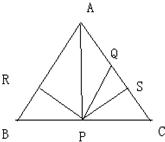 24、如圖所示,△ABC為等邊三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,有下面四個結論:
24、如圖所示,△ABC為等邊三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,有下面四個結論:查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com