
【題目】如圖1,拋物線y=﹣x2+bx+c與x軸交于A(2,0),B(﹣4,0)兩點.
(1)求該拋物線的解析式;
(2)若拋物線交y軸于C點,在該拋物線的對稱軸上是否存在點Q,使得△QAC的周長最小?若存在,求出Q點的坐標;若不存在,請說明理由.
(3)在拋物線的第二象限圖象上是否存在一點P,使得△PBC的面積最大?若存在,求出點P的坐標及△PBC的面積最大值;若不存,請說明理由.

【答案】(1)、y=﹣x2﹣2x+8;(2)、Q(﹣1,6);(3)、(﹣2,8)
【解析】
試題分析:(1)、直接利用待定系數求出二次函數解析式即可;(2)、首先求出直線BC的解析式,再利用軸對稱求最短路線的方法得出答案;(3)、根據S△BPC=S四邊形BPCO﹣S△BOC=S四邊形BPCO﹣16,得出函數最值,進而求出P點坐標即可.
試題解析:(1)、將A(2,0),B(﹣4,0)代入得:![]() , 解得:
, 解得:![]() ,
,
則該拋物線的解析式為:y=﹣x2﹣2x+8;
(2)、如圖1,點A關于拋物線對稱軸的對稱點為點B,設直線BC的解析式為: y=kx+d, 將點B(﹣4,0)、C(0,8)代入得:![]() , 解得:
, 解得:![]() ,
,
故直線BC解析式為:y=2x+8, 直線BC與拋物線對稱軸 x=﹣1的交點為Q,此時△QAC的周長最小.
解方程組![]() 得:
得:![]() 則點Q(﹣1,6)即為所求;
則點Q(﹣1,6)即為所求;
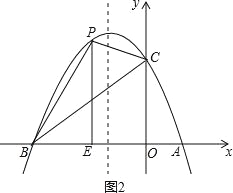
(3)、如圖2,過點P作PE⊥x軸于點E,
P點(x,﹣x2﹣2x+8)(﹣4<x<0) ∵S△BPC=S四邊形BPCO﹣S△BOC=S四邊形BPCO﹣16
若S四邊形BPCO有最大值,則S△BPC就最大
∴S四邊形BPCO=S△BPE+S直角梯形PEOC=![]() BEPE+
BEPE+![]() OE(PE+OC)=
OE(PE+OC)=![]() (x+4)(﹣x2﹣2x+8)+
(x+4)(﹣x2﹣2x+8)+![]() (﹣x)(﹣x2﹣2x+8+8)
(﹣x)(﹣x2﹣2x+8+8)
=﹣2(x+2)2+24,
當x=﹣2時,S四邊形BPCO最大值=24, ∴S△BPC最大=24﹣16=8, 當x=﹣2時,﹣x2﹣2x+8=8,
∴點P的坐標為(﹣2,8).



 陽光課堂課時優化作業系列答案
陽光課堂課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】小明和小剛進行賽跑訓練,他們選擇了一個土坡,按同一路線同時出發,從坡腳跑到坡頂再原路返回坡腳.他們倆上坡的平均速度不同,下坡的平均速度則是各自上坡平均速度的1. 5倍.設兩人出發x min后距出發點的距離為y m.圖中折線段OBA表示小明在整個訓練中y與x的函數關系,其中點A在x軸上,點B坐標為(2,480).
(1)點B所表示的實際意義是 ;
(2)求出AB所在直線的函數關系式;
(3)如果小剛上坡平均速度是小明上坡平均速度的一半,那么兩人出發后多長時間第一次相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某初一年級有500名同學,將他們的身高(單位:cm)數據繪制成頻率分布直方圖(如圖),若要從身高在 ![]() ,
, ![]() ,
, ![]() 三組內的學生中,用分層抽樣的方法選取30人參加一項活動,則從身高在
三組內的學生中,用分層抽樣的方法選取30人參加一項活動,則從身高在 ![]() 內的學生中選取的人數為 .
內的學生中選取的人數為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,AE⊥BC于點E,AF⊥CD交DC的延長線于點F,AE=4 cm,AF=5 cm,四邊形ABCD的周長為36 cm.求AB,BC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】政府為了更好地加強城市建設,就社會熱點問題廣泛征求市民意見,調查方式是發調查表,要求每位被調查人員只寫一個你最關心的有關城市建設的問題,經統計整理,發現對環境保護問題提出的最多,有700人,同時作出相應的條形統計圖,如圖所示,請回答下列問題.
(1)共收回調查表張;
(2)提道路交通問題的有人;
(3)請你把這個條形統計圖用扇形統計圖表示出來.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=k1x+b1與反比例函數y=![]() 的圖象及坐標軸依次相交于A、B、C、D四點,且點A坐標為(﹣3,
的圖象及坐標軸依次相交于A、B、C、D四點,且點A坐標為(﹣3,![]() ),點B坐標為(1,n).
),點B坐標為(1,n).
(1)求反比例函數及一次函數的解析式;
(2)求證:AC=BD;
(3)若將一次函數的圖象上下平移若干個單位后得到y=k1x+n,其與反比例函數圖象及兩坐標軸的交點仍然依次為A、B、C、D.(2)中的結論還成立嗎?請寫出理由,對于任意k<0的直線y=kx+b.(2)中的結論還成立嗎?(請直接寫出結論)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若直線y=kx+b經過第一、二、四象限,則k,b的取值范圍是( )
A. k>0, b>0 B. k>0,b<0 C. k<0,b>0 D. k<0,b<0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com