
已知直線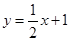 與
與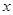 軸交于點
軸交于點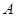 ,與
,與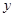 軸交于點
軸交于點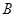 ,將三角形
,將三角形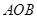 繞點
繞點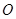 順時針旋轉90°,使點
順時針旋轉90°,使點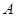 落在點
落在點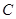 ,點
,點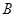 落在點
落在點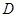 ,拋物線
,拋物線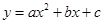 過點
過點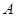 、
、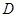 、
、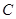 ,其對稱軸與直線
,其對稱軸與直線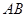 交于點
交于點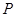 .
.
(1)求拋物線的表達式;
(2)求 的正切值;
的正切值;
(3)點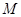 在
在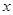 軸上,且△
軸上,且△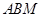 與△
與△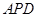 相似,求點
相似,求點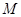 的坐標.
的坐標.
(1)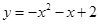 (2)
(2)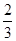 (3)
(3)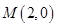 或(
或( ,0)
,0)
【解析】解:(1)由題意得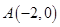 ,
,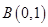
∵△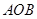 旋轉至△
旋轉至△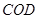 ,∴
,∴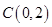 ,
,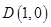 2分
2分
∵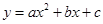 過點
過點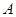 、
、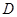 、
、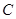 ,
,
∴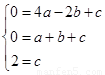 ,
,
∴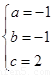 ,即拋物線是
,即拋物線是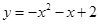 2分
2分
解:(2)設對稱軸與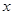 軸交點為
軸交點為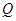 .
.
∵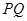 //
// 軸,
軸,
∴∠ =∠
=∠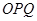
∵拋物線的對稱軸為直線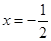 1分
1分
∴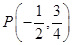 1分
1分
∴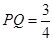 ,
,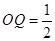 ,在Rt△
,在Rt△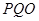 中,
中,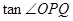 =
=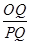 =
=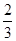
∴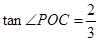 2分
2分
解:(3)∵點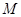 在
在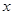 軸上,且△
軸上,且△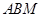 與△
與△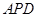 相似,
相似,
∴點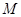 必在點
必在點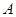 的右側
的右側
∵∠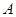 =∠
=∠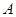 ,
,
∴ 或
或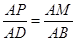 ,
2分
,
2分
即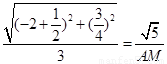 或
或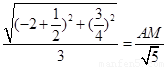 ,
,
∴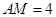 或
或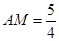
∴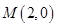 或(
或( ,0)
1分
,0)
1分
(1)先求出點A、B的坐標,再根據旋轉的性質求出點C、D的坐標,然后利用待定系數法求拋物線解析式即可;
(2)根據拋物線解析式求出對稱軸解析式,然后求出點P的坐標,過點P作PQ⊥x軸,則PQ∥y軸,根據兩直線平行,內錯角相等可得∠OPQ=∠POC,然后利用點P的坐標,根據銳角的正切值的定義列式計算即可得解;
(3)根據點M在x軸上,且△ABM與△APD相似可知,點M一定在點A的右側,然后求出AP、AB、AD的長度,因為對應邊不明確,所以分①AP和AB是對應邊,②AP和AM是對應邊,然后根據相似三角形對應邊成比例列式求出AM的長度,再根據點A的坐標求解即可.


科目:初中數學 來源: 題型:
已知直線![]() 與
與![]() 軸交于點A(-4,0),與
軸交于點A(-4,0),與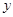 軸交于點B.
軸交于點B.

1.求b的值
2.把△AOB繞原點O順時針旋轉90°后,點A落在![]() 軸的
軸的![]() 處,點B若在
處,點B若在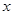 軸的
軸的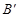 處;
處;
①求直線![]() 的函數關系式;
的函數關系式;
②設直線AB與直線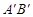 交于點C,矩形PQMN是△
交于點C,矩形PQMN是△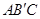 的內接矩形,其中點P,Q在線段
的內接矩形,其中點P,Q在線段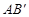 上,點M在線段
上,點M在線段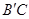 上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.
上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
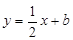 與
與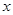 軸交于點A(-4,0),與
軸交于點A(-4,0),與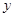 軸交于點B.
軸交于點B.
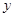 軸的
軸的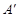 處,點B若在
處,點B若在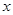 軸的
軸的 處;
處;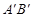 的函數關系式;
的函數關系式;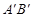 交于點C,矩形PQMN是△
交于點C,矩形PQMN是△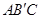 的內接矩形,其中點P,Q在線段
的內接矩形,其中點P,Q在線段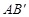 上,點M在線段
上,點M在線段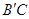 上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.
上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.查看答案和解析>>
科目:初中數學 來源:2012屆上海市楊浦初三基礎測試數學試卷(帶解析) 題型:解答題
已知直線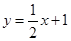 與
與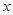 軸交于點
軸交于點 ,與
,與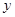 軸交于點
軸交于點 ,將三角形
,將三角形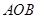 繞點
繞點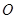 順時針旋轉90°,使點
順時針旋轉90°,使點 落在點
落在點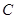 ,點
,點 落在點
落在點 ,拋物線
,拋物線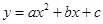 過點
過點 、
、 、
、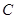 ,其對稱軸與直線
,其對稱軸與直線 交于點
交于點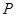 .
.
(1)求拋物線的表達式;
(2)求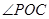 的正切值;
的正切值;
(3)點 在
在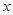 軸上,且△
軸上,且△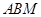 與△
與△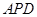 相似,求點
相似,求點 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源:2013屆福建省泉州市八年級期中考數學試卷(解析版) 題型:解答題
已知直線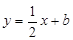 與
與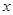 軸交于點A(-4,0),與
軸交于點A(-4,0),與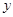 軸交于點B.
軸交于點B.

1.求b的值
2.把△AOB繞原點O順時針旋轉90°后,點A落在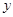 軸的
軸的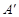 處,點B若在
處,點B若在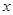 軸的
軸的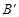 處;
處;
①求直線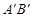 的函數關系式;
的函數關系式;
②設直線AB與直線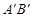 交于點C,矩形PQMN是△
交于點C,矩形PQMN是△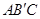 的內接矩形,其中點P,Q在線段
的內接矩形,其中點P,Q在線段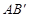 上,點M在線段
上,點M在線段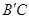 上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.
上,點N在線段AC上.若矩形PQMN的兩條鄰邊的比為1∶2,試求矩形PQMN的周長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com