
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD.若點B的坐標為(2,0),則點C的坐標為( ).
x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD.若點B的坐標為(2,0),則點C的坐標為( ).

A.(﹣1,![]() ) B.(﹣2,
) B.(﹣2,![]() )
)
C.(﹣![]() ,1) D.(﹣
,1) D.(﹣![]() ,2)
,2)
【答案】A.
【解析】
試題分析:作CH⊥x軸于H,如圖,
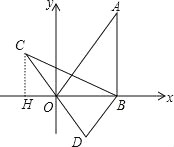
先根據一次函數圖象上點的坐標特征確定A(2,2![]() ),再利用旋轉的性質得BC=BA=2
),再利用旋轉的性質得BC=BA=2![]() ,∠ABC=60°,則∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三邊的關系可計算出CH=
,∠ABC=60°,則∠CBH=30°,然后在Rt△CBH中,利用含30度的直角三角形三邊的關系可計算出CH=![]() BC=
BC=![]() ,BH=
,BH=![]() CH=3,所以OH=BH﹣OB=3﹣2=1,于是可寫出C點坐標.先作CH⊥x軸于H,如圖,∵點B的坐標為(2,0),AB⊥x軸于點B,∴A點橫坐標為2,當x=2時,y=
CH=3,所以OH=BH﹣OB=3﹣2=1,于是可寫出C點坐標.先作CH⊥x軸于H,如圖,∵點B的坐標為(2,0),AB⊥x軸于點B,∴A點橫坐標為2,當x=2時,y=![]() x=2
x=2![]() ,∴A(2,2
,∴A(2,2![]() ),∵△ABO繞點B逆時針旋轉60°得到△CBD,∴BC=BA=2
),∵△ABO繞點B逆時針旋轉60°得到△CBD,∴BC=BA=2![]() ,∠ABC=60°,∴∠CBH=30°,在Rt△CBH中,CH=
,∠ABC=60°,∴∠CBH=30°,在Rt△CBH中,CH=![]() BC=
BC=![]() ,BH=
,BH=![]() CH=3,OH=BH﹣OB=3﹣2=1,∴C(﹣1,
CH=3,OH=BH﹣OB=3﹣2=1,∴C(﹣1,![]() ).故選:A.
).故選:A.


 智慧小復習系列答案
智慧小復習系列答案科目:初中數學 來源: 題型:
【題目】某初一年級有500名同學,將他們的身高(單位:cm)數據繪制成頻率分布直方圖(如圖),若要從身高在 ![]() ,
, ![]() ,
, ![]() 三組內的學生中,用分層抽樣的方法選取30人參加一項活動,則從身高在
三組內的學生中,用分層抽樣的方法選取30人參加一項活動,則從身高在 ![]() 內的學生中選取的人數為 .
內的學生中選取的人數為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC的三邊分別為a,b,c,△A'B'C'的三邊分別為a',b',c',且有a2+a'2+b2+b'2+c2+c'2=2ab'+2bc'+2ca',則△ABC與△A'B'C'( )
A. 一定全等 B. 不一定全等 C. 一定不全等 D. 無法確定
查看答案和解析>>
科目:初中數學 來源: 題型:
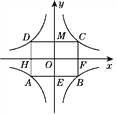
【題目】如圖,是由四條曲線圍成的廣告標志,建立平面直角坐標系,雙曲線對應的函數表達式分別為y=-![]() ,y=
,y=![]() .現用四根鋼條固定這四條曲線,這種鋼條加工成長方形產品按面積計算,每單位面積25元,請你幫助工人師傅計算一下,所需鋼條一共花多少錢?
.現用四根鋼條固定這四條曲線,這種鋼條加工成長方形產品按面積計算,每單位面積25元,請你幫助工人師傅計算一下,所需鋼條一共花多少錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若直線y=kx+b經過第一、二、四象限,則k,b的取值范圍是( )
A. k>0, b>0 B. k>0,b<0 C. k<0,b>0 D. k<0,b<0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com