
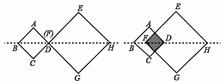
如圖,四邊形ABCD是邊長為1 的正方形,四邊形EFGH是邊長為2的正方形,點D與點F重合,點B,D(F),H在同一條直線上,將正方形ABCD沿F→H方向平移至點B與點H重合時停止,設點D、F之間的距離為x,正方形ABCD與正方形EFGH重疊部分的面積為y,則能大致反映y與 x之間函數關系的圖象是( )
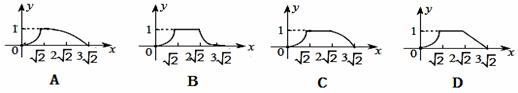
 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
某手機店經銷的Iphone5手機二月售價比一月每臺降價500元.如果賣出相同數量的Iphone5手機,那么一月銷售額為9萬元,二月銷售額只有8萬元.
(1)一月Iphone5手機每臺售價為多少元?
(2)為了擴大經營,該店計劃三月購進Iphone5s手機銷售,已知Iphone5每臺進價為3500元,Iphone5s每臺進價為4000元,該手機店打算用10萬元再購進一批Iphone5和Iphone5s,問購進Iphone5手機10臺后至多還能購進多少臺Iphone5s?
查看答案和解析>>
科目:初中數學 來源: 題型:
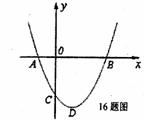
如圖,二次函數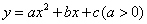 圖象的頂點為
圖象的頂點為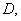 其圖象與
其圖象與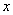 軸的交點為
軸的交點為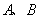 ,對稱軸為直線x=1,與
,對稱軸為直線x=1,與 軸負半軸交于點
軸負半軸交于點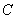 ,且OB=OC>2, 下面五個結論:
,且OB=OC>2, 下面五個結論:
①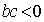 , ②
, ②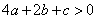 , ③
, ③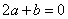 , ④
, ④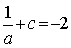 ,
,
⑤一元二次方程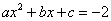 必有兩個不相等的實數根.其中正確的結論是_ .
必有兩個不相等的實數根.其中正確的結論是_ .
(只填序號,多填一個不得分,每少填一個扣2分)
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖1至圖4中,兩平行線AB、CD間的距離均為6,點M為AB上一定點.
思考:如圖1,圓心為0的半圓形紙片在AB,CD之間(包括AB,CD),其直徑MN在AB上,MN=8,點P為半圓上一點,設∠MOP=α。
當α=__ __度時,點P到CD的距離最小,最小值為__  __.
__.
探究一:在圖1的基礎上,以點M為旋轉中心,在AB,CD 之間順時針旋轉該半圓形紙片,直到不能再轉動為止,如圖2,得到最大旋轉角∠BMO=_ __度,此時點N到C D的距離是__ __.
D的距離是__ __.
探究二:將如圖1中的扇形紙片NOP按下面對α的要求剪掉,使扇形紙片MOP繞點M在AB,CD之間順時針旋轉。
(1)如圖3,當α=60°時,求 在旋轉過程中,點P到CD的最小距離,并請指出旋轉角∠BMO的最大值;
在旋轉過程中,點P到CD的最小距離,并請指出旋轉角∠BMO的最大值;
(2)如圖4,在扇形紙片MOP旋轉過程中,要保證點P能落在直線CD上,請直接確定α的最大值=__ __.

查看答案和解析>>
科目:初中數學 來源: 題型:
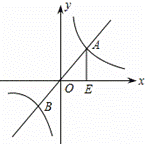
如圖,已知函數y=2x和函數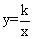 的圖象交于A、B兩點,過點A作AE⊥x軸于點E,若△AOE的面積為4,P是坐標平面上的點,且以點B、O、E、P為頂點的四邊形是平行四邊形,則滿足條件的P點坐標是 .
的圖象交于A、B兩點,過點A作AE⊥x軸于點E,若△AOE的面積為4,P是坐標平面上的點,且以點B、O、E、P為頂點的四邊形是平行四邊形,則滿足條件的P點坐標是 .
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com