
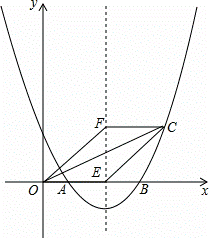
如圖,拋物線y=ax2+bx+2與x軸交于點A(1,0)和B(4,0).
(1)求拋物線的解析式;
(2)若拋物線的對稱軸交x軸于點E,點F是位于x軸上方對稱軸上一點,FC∥x軸,與對稱軸右側的拋物線交于點C,且四邊形OECF是平行四邊形,求點C的坐標;
(3)在(2)的條件下,拋物線的對稱軸上是否存在點P,使△OCP是直角三角形?若存在,求出點P的坐標;若不存在,請說明理由.
解:(1)把點A(1,0)和B(4,0)代入y=ax2+bx+2得,
 ,
,
解得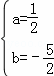 ,
,
所以,拋物線的解析式為y= x2﹣
x2﹣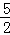 x+2;
x+2;
(2)拋物線的對稱軸為直線x=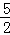 ,
,
∵四邊形OECF是平行四邊形,
∴點C的橫坐標是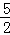 ×2=5,
×2=5,
∵點C在拋物線上,
∴y= ×52﹣
×52﹣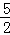 ×5+2=2,
×5+2=2,
∴點C的坐標為(5,2);
(3)設OC、EF的交點為D,
∵點C的坐標為(5,2),
∴點D的坐標為(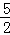 ,1),
,1),
①點O是直角頂點時,易得△OED∽△PEO,
∴ =
= ,
,
即 =
= ,
,
解得PE= ,
,
所以,點P的坐標為( ,﹣
,﹣ );
);
②點C是直角頂點時,同理求出PF= ,
,
所以,PE= +2=
+2= ,
,
所以,點P的坐標為( ,
, );
);
③點P是直角頂點時,由勾股定理得,OC= =
= ,
,
∵PD是OC邊上的中線,
∴PD= OC=
OC= ,
,
若點P在OC上方,則PE=PD+DE= +1,
+1,
此時,點P的坐標為( ,
, ),
),
若點P在OC的下方,則PE=PD﹣DE= ﹣1,
﹣1,
此時,點P的坐標為( ,
, ),
),
綜上所述,拋物線的對稱軸上存在點P( ,﹣
,﹣ )或(
)或( ,
, )或(
)或( ,
, )或(
)或( ,
, ),使△OCP是直角三角形.
),使△OCP是直角三角形.



科目:初中數學 來源: 題型:
某品牌電插座抽樣檢查的合格率為99%,則下列說法中正確的是······················ ( )
A.購買100個該品牌的電插座,一定有99個合格
B.購買1000個該品牌的電插座,一定有10不個合格
C.購買20個該品牌的電插座,一定都合格
D.即使購買1個該品牌的電插座,也可能不合格
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,函數y=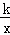 的圖象過點A(1,2).
的圖象過點A(1,2).
(1) 求該函數的解析式;
求該函數的解析式;
(2)過點A分別向x軸和y軸作垂線,垂足為B和C,求四邊形ABOC的面積;
(3)求證:過此函數圖象上任意一點分別向x軸和y軸作垂線,這兩條垂線與兩坐標軸所圍成矩形的面積為定值.

查看答案和解析>>
科目:初中數學 來源: 題型:
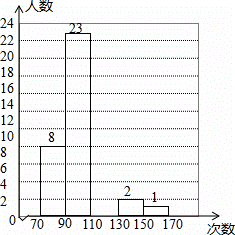
某校為了了解學生大課間活動的跳繩情況,隨機抽取了50名學生每分鐘跳繩的次數進行統計,把統計結果繪制成如表和直方圖.
| 次數 | 70<x<90 | 90<x<110 | 110≤x<130 | 130≤x<150 | 150≤x<170 |
| 人數 | 8 | 23 | 16 | 2 | 1 |
根據所給信息,回答下列問題:
(1)本次調查的樣本容量是 ;
(2)本次調查中每分鐘跳繩次數達到110次以上(含110次)的共有的共有 人;
(3)根據上表的數據補全直方圖;
(4)如果跳繩次數達到130次以上的3人中有2名女生和一名男生,學校從這3人中抽取2名學生進行經驗交流,求恰好抽中一男一女的概率(要求用列表法或樹狀圖寫出分析過程).
查看答案和解析>>
科目:初中數學 來源: 題型:
PM2.5是指大氣中直徑小于或等于0.000 002 5米的顆粒物,將0.000 002 5用科學記數法表示為( )
|
| A. | 0.25×10﹣5 | B. | 2.5×10﹣5 | C. | 2.5×10﹣6 | D. | 2.5×10﹣7 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com