
【題目】如圖,分別延長ABCD的邊CD,AB到E,F,使DE=BF,連接EF,分別交AD,BC于G,H,連結CG,AH.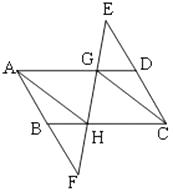
求證:CG∥AH.
【答案】證明:在ABCD中,
AB∥CD,AD∥CB ,AD=CB,
∴∠E=∠F,∠EDG=∠DCH=∠FBH,
又 DE=BF ,
∴△EGD≌△FHB(AAS) ,
∴DG=BH,
∴AG=HC ,
又∵AD∥CB,
∴四邊形AGCH為平行四邊形,
∴AH∥CG.
【解析】方法不唯一,如:證明四邊形AGCH為平行四邊形,可通過證明△EGD≌△FHB,已知DE=BF,再根據ABCD得出兩組角相等即可證明△EGD≌△FHB,即可求證AH∥CG.
【考點精析】利用平行四邊形的判定與性質對題目進行判斷即可得到答案,需要熟知若一直線過平行四邊形兩對角線的交點,則這條直線被一組對邊截下的線段以對角線的交點為中點,并且這兩條直線二等分此平行四邊形的面積.


科目:初中數學 來源: 題型:
【題目】已知∠MAN=135°,正方形ABCD繞點A旋轉.
(1)當正方形ABCD旋轉到∠MAN的外部(頂點A除外)時,AM,AN分別與正方形ABCD的邊CB,CD的延長線交于點M,N,連接MN.
①如圖1,若BM=DN,則線段MN與BM+DN之間的數量關系是 ;
②如圖2,若BM≠DN,請判斷①中的數量關系是否仍成立?若成立,請給予證明;若不成立,請說明理由;
(2)如圖3,當正方形ABCD旋轉到∠MAN的內部(頂點A除外)時,AM,AN分別與直線BD交于點M,N,探究:以線段BM,MN,DN的長度為三邊長的三角形是何種三角形,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
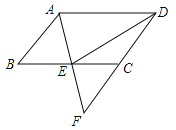
【題目】如圖,在ABCD中,E是BC的中點,連接AE并延長交DC的延長線于點F.
(1)求證:AB=CF;
(2)連接DE,若AD=2AB,求證:DE⊥AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點P(1,1),N(2,0),△MNP和△M1N1P1的頂點都在格點上,△MNP與△M1N1P1是關于某一點中心對稱,則對稱中心的坐標為 .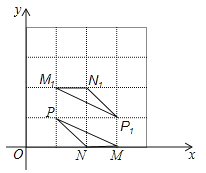
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com