解:(1)將點D(6,1)的坐標代入反比例函數解析式可得:1=
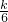
,
解得:k=6;
(2)過點C作CF⊥DB,交DB的延長線于點F,

則S
△BCD=

BD×CF=

×6×(1-C
縱)=12,
解得:C
縱=-3,
代入y=

,可得點C的坐標為(-2,-3),
設直線CD的解析式為:y=kx+b,
則

,
解得:

,
故直線CD的解析式為y=

x-2.
(3)設點C的坐標為(m,

),直線CD的解析式為y=ax+c,
則

,
解得:

,
即直線CD的解析式為:y=-

x+

,
令y=0,則x=6+m,則點E的坐標為(6+m,0),
故EA=6+m-m=6,
∵BD=EA=6,BD∥EA,
∴四邊形ABDE是平行四邊形,
∴AB∥DE,
∴∠BAO=∠AEC,
又∵∠AOB=∠EAC=90°,
∴△AOB∽△EAC.
分析:(1)將點D的坐標代入反比例函數解析式即可求出k的值;
(2)根據△BCD的面積為12,求出點C的縱坐標,代入反比例函數解析式可得出點C的坐標,繼而利用待定系數法求直線CD的解析式;
(3)設點C的坐標為(m,

),求出直線CD的解析式,繼而得出點E的坐標,然后判斷出BD=AE,可得出四邊形ABDE是平行四邊形,從而得出AB∥CD,這樣即可證明△AOB∽△EAC.
點評:本題考查了反比例函數綜合題,涉及了待定系數法求函數解析式、相似三角形的判定,難點在第三問,解答此類題目注意大膽設出點的坐標,通過最終消去得解.

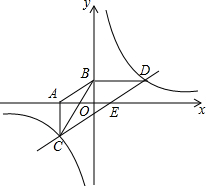 如圖,已知點D(6,1)是反比例函數
如圖,已知點D(6,1)是反比例函數 (k≠0)圖象上的一點,點C是該函數在第三象限分支上的動點,過C、D分別作CA⊥x軸,DB⊥y軸,垂足分別為A、B,連結AB,BC.
(k≠0)圖象上的一點,點C是該函數在第三象限分支上的動點,過C、D分別作CA⊥x軸,DB⊥y軸,垂足分別為A、B,連結AB,BC.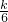 ,
,
 BD×CF=
BD×CF= ×6×(1-C縱)=12,
×6×(1-C縱)=12, ,可得點C的坐標為(-2,-3),
,可得點C的坐標為(-2,-3), ,
, ,
, x-2.
x-2. ),直線CD的解析式為y=ax+c,
),直線CD的解析式為y=ax+c, ,
, ,
, x+
x+ ,
, ),求出直線CD的解析式,繼而得出點E的坐標,然后判斷出BD=AE,可得出四邊形ABDE是平行四邊形,從而得出AB∥CD,這樣即可證明△AOB∽△EAC.
),求出直線CD的解析式,繼而得出點E的坐標,然后判斷出BD=AE,可得出四邊形ABDE是平行四邊形,從而得出AB∥CD,這樣即可證明△AOB∽△EAC.

 通城學典默寫能手系列答案
通城學典默寫能手系列答案 如圖,已知點A、B、C、D均在已知圓上,AD∥BC,AC平分∠BCD,∠ADC=120°,四邊形ABCD的周長為10cm.圖中陰影部分的面積為( )
如圖,已知點A、B、C、D均在已知圓上,AD∥BC,AC平分∠BCD,∠ADC=120°,四邊形ABCD的周長為10cm.圖中陰影部分的面積為( ) 如圖,已知點D為△ABC中AC邊上一點,且AD:DC=3;4,設
如圖,已知點D為△ABC中AC邊上一點,且AD:DC=3;4,設